It’s that time of the year again when primary teachers shift their focus to collating assessment data to write end of semester reports to parents. So how do we make judgements in mathematics? And what does ‘high’ or ‘outstanding’ look like in mathematics?
In NSW schools (NSW Department schools specifically as this is where my experience is) our requirements when reporting to parents involves the use of a five-point achievement A to E grading scale (NESA common grade scale) or the use of the matched wording scale Limited to Outstanding (NSW Department of Education policy).
There are some fundamental aspects to the use of this grading scale that NESA points out on their websites about the grades themselves and about reporting on the grades. I know from personal experience, and from talking with numerous teachers, that the interpretation of this information varies within and between schools leading to inconsistent use of the grading scale.
From reading NESA’s information, the key points that I believe need to become consistent are:
- 1. A and B grades are not just for students working beyond their stage of learning. The A to E grading scale is for use WITHIN a stage of learning e.g. Stage 2. That is, I can award A and B grades to students in my class based on their achievement of Stage 2 outcomes. I will elaborate later in this blog as to what those higher levels may look like. NESA does state that students who may be being exposed to teaching of higher content (e.g. Stage 3) would receive say an A in Stage 2 on their report and may receive comments regarding achievement of the higher stage content also. This does not mean that they are the only students to receive As and Bs.
- 2. I can award an A or B at any point during a students’ stage of learning. If you teach a straight year 3, you can still award students in your class with an A or B if they are displaying high or outstanding understanding and application of the content. This is because
“the assessment information they have collected for each student [is] up to that point in time.”
(NESA)
The grade is based on the content students have been exposed to- we are not making judgements against end-of-stage standards,
“give the grade that best matches the standard achieved so far.”
(NESA)
- 3. A C is a C everywhere.
“Grades are given for individual achievement. Students receive the grade that best matches the standard of their achievement.”
(NESA)
The judgement should be made against the standards, that is, the NSW K-6 syllabus outcomes, not compared with, or to, other students. This means you may have a class where many students receive As and Bs or where all students receive Cs. The intent is not to ‘grade’ your class then ‘divvy-up’ percentages of each grade A to E or give a set number of each grade.
“Teachers are not limited to set numbers of each grade within their class or school.”
(NESA)
- 4. Grade judgements form one part of reporting to parents, decisions about grades are best made via numerous work/ assessment samples, not a single test. Assessment data used for reporting needs to be
“built up over time and [come from] different situations.”
(NESA)
Teachers are to make on-balanced judgements based on their knowledge of the syllabus outcomes.
“An on-balance judgement does not just focus on a single piece of work.”
(NESA)
NESA encourages teachers to use assessment for learning practices over time to collect data to make grading judgements. When we use ongoing assessment practices (including self-assessment and peer assessment) that assess students before, during and after learning sequences, it means we can rely on those assessments already gathered to make valid judgements. This stops the necessity for end of Term or end of year one-off ‘tests’ that may cover multiple areas (particularly in mathematics) in a shallow fashion that often do not reflect what the students actually know.
So, what does this mean for mathematics specifically? What are we looking for in students’ work samples that may indicate they are working above a ‘sound’ grade?
“Every task should be good enough to be an assessment task” Christine Mae, formative assessment as a daily practice. #MANSW18
— katherin cartwright (@kath_cartwright) September 15, 2018
Well first of all, the tasks we provide need to have a low floor – to provide opportunities for students to display their content knowledge and also have a high ceiling – so students can show their application of mathematics skills and processes. I refer back to tweet I posted in a previous blog regarding the quality of tasks. Christine Mae in a presentation I attended at the MANSW conference stated that all tasks should be assessment worthy. When we think of our activities or tasks or lessons this way, it makes assessing and analysing work samples easier and broadens the scope of what efficient and effective strategies students have the opportunity to display.
When we drill down into what an A (Outstanding) or B (High) means, the grade descriptions give us a clear view of what these students may be doing:
A grade
The student has an extensive knowledge and understanding of the content and can readily apply this knowledge. In addition, the student has achieved a very high level of competence in the processes and skills and can apply these skills to new situations.
B grade
The student has a thorough knowledge and understanding of the content and a high level of competence in the processes and skills. In addition, the student is able to apply this knowledge and these skills to most situations.
Within these grade descriptors what jumps out to me is the word ‘apply’. This word is not used within the C, D or E grade description so that tells me it’s an important distinction between C (sound) and B and A (high and outstanding respectively).
Take this task from the NSW Department of Education resource Teaching Measurement for example.
This task is a rich task in the sense that it allows students to use various strategies to solve the task. There are a number of changes you could make to the task to create a lower floor or a higher ceiling.
To create a lower floor, you could ask students to…
- Create just one prism with a volume of 36 cubic centimetres
Or change the numerical value to a smaller number, for example, 12 cubic centimetres. Or students could explore creating prisms without specifying the size.
To extend the task or create a high ceiling, the task needs to focus on application (transference) of the skill, either within the same area of mathematics…
- Explore prisms with a volume of 20 cubic centimetres, how many of those can you create? What might be some other numbers you can use that create multiple prisms?
… between areas of mathematics….
- Explain how you created your prisms. Where did you start? What other mathematics skills and strategies did you use to solve the task? How could you apply your strategy to find different ways to make rectangles that have an area of 36 square centimetres?
Or to other situations beyond mathematics or into areas of mathematics that may not have been addressed, yet…
- Have you found all the solutions? Are there more ways to create prisms with a volume of 36 cubic centimetres? Are there any numbers that only have one way to create a prism? If yes, prove it.
- You are a builder who is creating a model of a new housing area. There needs to be 10 different buildings (prisms) all with a volume of 36 cubic centimetres. What might your buildings look like? (Enabling prompt: You are allowed to change the orientation of your prisms to make them ‘different’)
The higher grades also talk about process and skills as well as content knowledge. Processes and skills are mentioned in all grades, but in B and A it is about the level of competence. In mathematics this could be interpreted as:
- the level of confidence or efficiency with a variety of strategies (problem solving) or
- a students’ ability to justify, see patterns, or make generalisations (reasoning) or
- their capacity to share their knowledge (communicating).
To me, to say a student is working at a B or A grade, I would focus on their working mathematically processes. These components of the mathematics syllabus is what connects all of the other parts of mathematics into a cohesive whole. Once students can communicate, problem solve and reason about their content knowledge, they are often showing higher levels of mathematical thinking (application) than just being able to use a procedure or apply a skill in a single situation or problem. We are talking about mathematical proficiency. The more sophisticated their processes are for understanding and applying mathematical knowledge, the more proficient they are. Tasks that focus on working mathematically processes provide the opportunities teachers need to see these higher order skills. The prism task above has some of these opportunities.
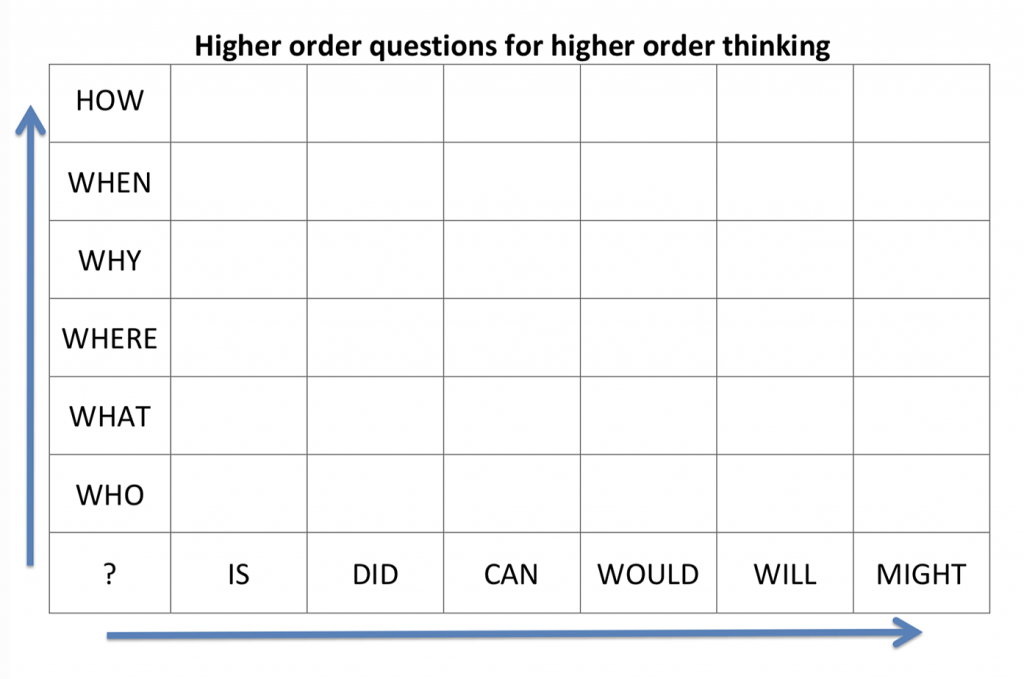
Anne Prescott from UTS shared the framework below at a session I attended. It is a nice, simple representation of the types of questions we can ask in the mathematics classroom and how tweaking the questions we pose can increase students’ higher order thinking.
As you move up and along each axis, the types of questions become more open and provide more opportunities for multiple solutions and therefore increases the opportunities for students to work mathematically. Shifting from asking “what did you do?” to “why might you do it that way?” also shifts students’ responses from stating the procedures or steps they used to sharing the efficiency of their strategy, explaining why it works.
Time will always be a factor for teachers in being able to create assessments. Also, the current pressure on teachers to show evidence for accountability of how they teach and assess students may be hindering teachers’ interest in being more experimental or innovative with their assessment strategies. What is encouraging, is the way in which teachers continue to want to learn more about being better at their chosen vocation and the ways in which they form professional communities of practice to share effective assessment and reporting strategies.
It is also important to note that NESA, when talking about providing grades for students, places a high value on teachers’ “on-balance judgements” as a key professional skill. Wouldn’t it be great if everyone valued teachers’ professional judgement, viewing their judgements and informal observations as equally important and valid as written formal assessment activities.