There’s maths in that!

Patterns or patterning is one of the ‘big ideas’ in mathematics. Noticing patterns in mathematics and seeing relationships between numbers helps students make generalisations. One simple example is noticing that 2, 4, 6, 8, 10, 12, 14, 16, 18, 20 … are all even numbers. And then generalising that all numbers that end in a 0, 2, 4, 6, or 8 must be even. Finding pattern examples in nature supports the importance of patterns giving structure and meaning. Fibonacci number patterns can be observed in peacock feathers, or pinecones or sunflowers. Vi Hart has some great videos on patterns in nature, her one on pinecones is amazing.

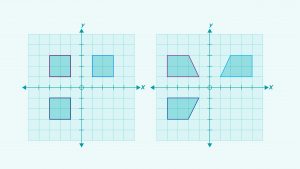
Shape transformations including reflection and symmetry can be explored at a young age with students. Visualising what a shape looks like in different orientations is an important precursor skill to being about to transform shapes mentally (reflect, rotate, translate) in more abstract ways in upper primary. Students can notice reflections and symmetry in nature, identifying where the ‘line’ of reflection or symmetry is, as well as outlining (tracing, gesturing or drawing over) the shapes that are reflected or repeated. In mathematics, shapes retain their features when reflected, rotated or translated (slide) as part of ‘rigid’ transformations. However, you could explore situations in the real world where shape and size may not be retained such as in shadows at different times of the day.

Comparison is another ‘big idea’ in mathematics. Noticing features of an object, or objects, and comparing the objects based on a particular attribute (eg length, area, volume, mass) to notice how they differ is a fundamental understanding of measurement concepts. Students begin by being able to identify the attribute being measured, eg in this photo’s case length, to answer: how long is the centipede compared with the leaf? or how much longer is the leaf than the centipede? or which is longer the centipede or the leaf? or can you find something shorter than the centipede? 

In these questions I have highlighted some of the comparative language we expect students to use when comparing and ordering objects in measurement. Note: Having the physical items is particularly useful when exploring measurement concepts. I can only compare the leaf and the centipede to myself or other objects if they are in front of me. It is not recommended to use images for discussing volume or mass (weight) concepts.

Combining mathematics and art concepts is an authentic way to integrate learning areas. This integration has the additional benefit of reflecting how mathematics is used by artists, designers, architects and engineers for functional, or aesthetic purposes. The optical illusion carpet image here was in a hotel we stayed at. I often found it hard to walk on as the use of lines made the floor appear ‘lumpy’. To create optical illusions, mathematics is often used – including measurement, shape, angle and line concepts.

Lesson image from https://www.youcubed.org/tasks/optical-art-task/

The use of mathematics to make art really warrants its own blog looking at the use of the Golden Ratio, perspective, projective geometry, symmetry and tessellations by artists such as da Vinci, MC Escher, Max Ernst, Picasso, Mondrian just to name a few. Jo Boaler and colleagues have created a nice lesson for students to develop their own optical illusion art (pictured) that can be found on their youcubed website.

In mathematics, we use the pattern structure of an array (rows and columns) to count in multiples, find area, and to extend area to a third dimension to work out volume (row, column, layer). Packing and stacking items in rows or layers is cost-saving and space-efficient and is used in shops, vending machines, and supermarkets for example.

Structure is a ‘big idea’ in mathematics that is closely related to patterns. In mathematics, many of the structures we use are to keep ideas in order for others to understand and they are also used to organise (like in real life) things. Countable items or quantities are represented in various structural ways to make counting easier and patterns clearer. Think for a moment about combination of numbers that add to 10 (number bonds). Once they are written in order 10 + 0, 9 + 1, 8 + 2, 7 + 3, 6 + 4, 5 + 5 … there is a point where the pattern ‘turns’ and the same numbers begin to be used. Organising the combination in this way makes it easier to notice the pattern and to know ‘when you have them all’.

There are plenty of arrays in the environment such as in egg cartons, biscuit packets, chocolate blocks etc. Allowing students to try to count large quantities of things from a young age helps them see a need or purpose to organising them in a structural way to keep track of the count or make the count easier (eg by 2s, 5s, 10s or more).

There are many opportunities to see mathematics in the environment in school settings, at home and in the community. Some examples are natural and some are human-made, both show the beauty and functionality of mathematics. Using real-world examples provides students with a link between ‘school maths’ and the world, hopefully assisting them in thinking mathematics is relevant, thinking “I can see maths in that”.