Sometimes the best way to get faster is to slow down. I often use swimming as an analogy when talking about mathematical fluency. To become the fastest (‘best’) swimmer, you don’t just get in the pool and practice swimming fast. Swimming coaches break down aspects of each stroke, the arms, the legs, breathing etc and focus swimmers on improving each of these to then develop speed. Technique is the way to improving.
To me this is exactly what we as teachers should be doing to improve students’ mathematical fluency. The end result may be automaticity with known facts that can then be selected, used and justified for different problems but this isn’t where I start. Fast teaching or focusing on speed does not equate to fluency. In fact time pressure can have dire results for students’ attitudes towards to mathematics or towards themselves as learners.
“As students realize they cannot perform well on timed tests they start to develop anxiety and their mathematical confidence erodes.”
Fluency without fear, Jo Boaler
At a time where teaching seems to be busier than ever and our time for each learning area feels squeezed and ever diminishing due to other external factors, the best thing we can do for our students is slow down. In mathematics where new knowledge is built upon prior knowledge, taking the time to explore concepts deeply and holding back from making the connections for the students is paramount.
We want students to make the connections for themselves, within the mathematics, and between their ideas and the ideas of others. One way to do this is by using quick images in your classroom. I have mentioned quick images in two prior blogs; Reflecting and pondering and The importance of teaching not telling. I was first introduced to quick images by @janettebobis who shared with me Intentional Talk by @ekazemi and @alliosnhintz124 where quick images are used as part of the compare and contrast strategy. Quick images are also used regularly as part of Number talks and as lesson launch activities.
Quick images are not just about subitising
At a surface level, quick images provide teachers with information regarding students’ ability to visually identify a quantity or estimate a quantity without counting. However, taking the time to slow down and have students, all students, share firstly how many dots they see, then (after another quick look) how they see the dots allows for a deeper investigation into other concepts such as; combining, partitioning, grouping, halving, doubling, reflection, transformation, addition, subtraction, multiplication or area just to name a few!
@INV3_Math Quick Images equations are getting creative as we delve deeper into Unit 3. #math pic.twitter.com/uSqucnOK9g
— Weisenbach (@MTL_LM4Wizards) December 11, 2017
How would you count these eggs? 🥚 Many students counted by 3s or 6s. Would you then do repeated addition or multiplication? #4thgrade #4thgrademath #mentalmath #quickimages #mathisfun @LESDSchools @andersonLESD pic.twitter.com/6U46RH8a6k
— Laura Schmitz (@MsSchmitz_LESD) March 12, 2019
Recording student thinking about the representation is key
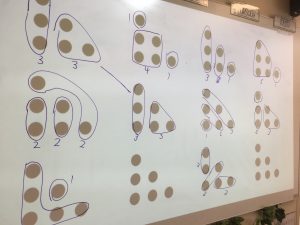
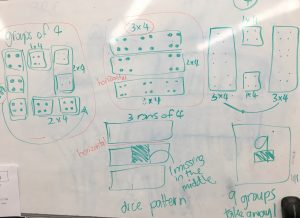
There are a few ways you can go about this, you could simply ask students to share how they see the dot arrangement as a conversation, you can ask students to share and you record on the images, or you can have students come out and share and draw how they saw the arrangement. The latter two are far more powerful to help students see the connections between the mathematical concepts (for example counting and partitioning) or between each others’ ideas (for example, “mine was almost the same as Zac’s because we both circled the first three dots”).
When you choose to record for the students, ensure you ask them as you are recording (and afterwards) if this is what they meant as sometimes we may interpret what they say differently. I also label each grouping they notice with its numerical value, I refrain from writing a number sentence below, this may be something the students choose to write later when comparing solutions or when they record on the image themselves. In this scenario, the student is learning to articulate what they saw and use mathematical words (usually involving positional language) to describe how they saw the image.
We now have a co-teaching model in which I watch Mrs. Courtney give a #numbertalk on day 1 and then I come in a give the same prompt on day 2. After that, we’ll get together and talk next steps. pic.twitter.com/fBhf9OYhk8
— Mr. Harris (@Mr_Harris_Math) February 21, 2019
When you allow the students to come out the front and draw and explain how they saw the image, you are giving them ownership over their learning and providing them with the space to communicate verbally and in writing their mathematical fluency. Allow as many students as possible to share their thinking (I often have a slide in my presentation with multiple versional of the image to support this – see below). This takes time, but it also is part of the teaching as the students start to look at the solutions of others and think (on the spot) of other solutions that haven’t been shared yet. These new ideas may not have been how they originally saw the image but it shows evidence of students’ abilities to switch between strategies and their fluidity with number structure and patterns.
Loved going back to a 4th grade class today and hearing them share their explanations for Quick Images. #GreatStrategies #jmiknights @MissGeletei @Inv3_Math pic.twitter.com/u9D5XnaqIQ
— + ‐ Dina O'Brien × ÷ (@Dina0Brien) October 1, 2018
This type of investigation may go beyond the 5 – 7 minutes you planned to spend on the quick image. That’s ok. Taking time to allow students to explore similarities and differences, justify which ones are the same and why, focuses on developing robust ways to solve problems. This links in aspects of reasoning as essential building blocks of mathematical fluency.