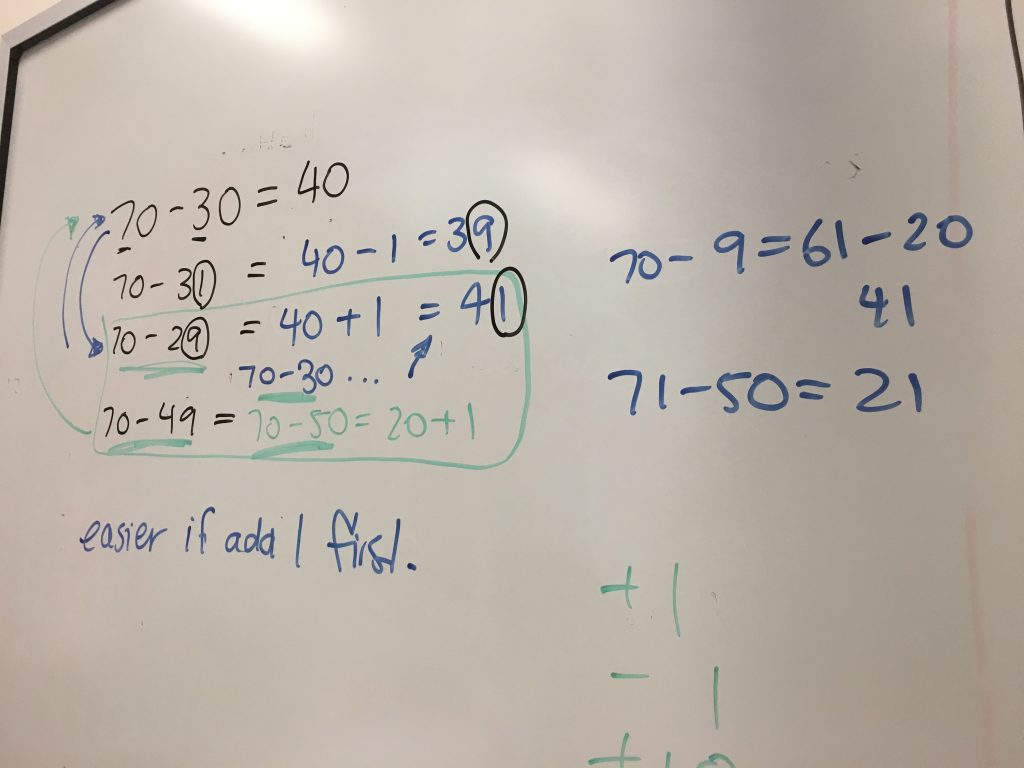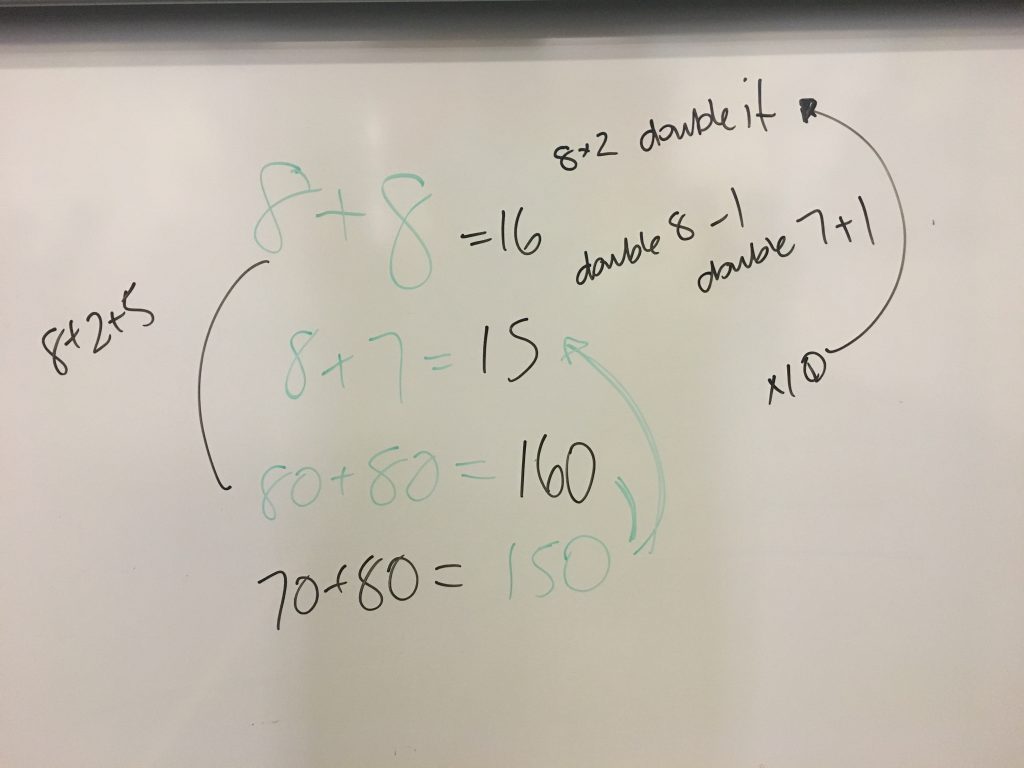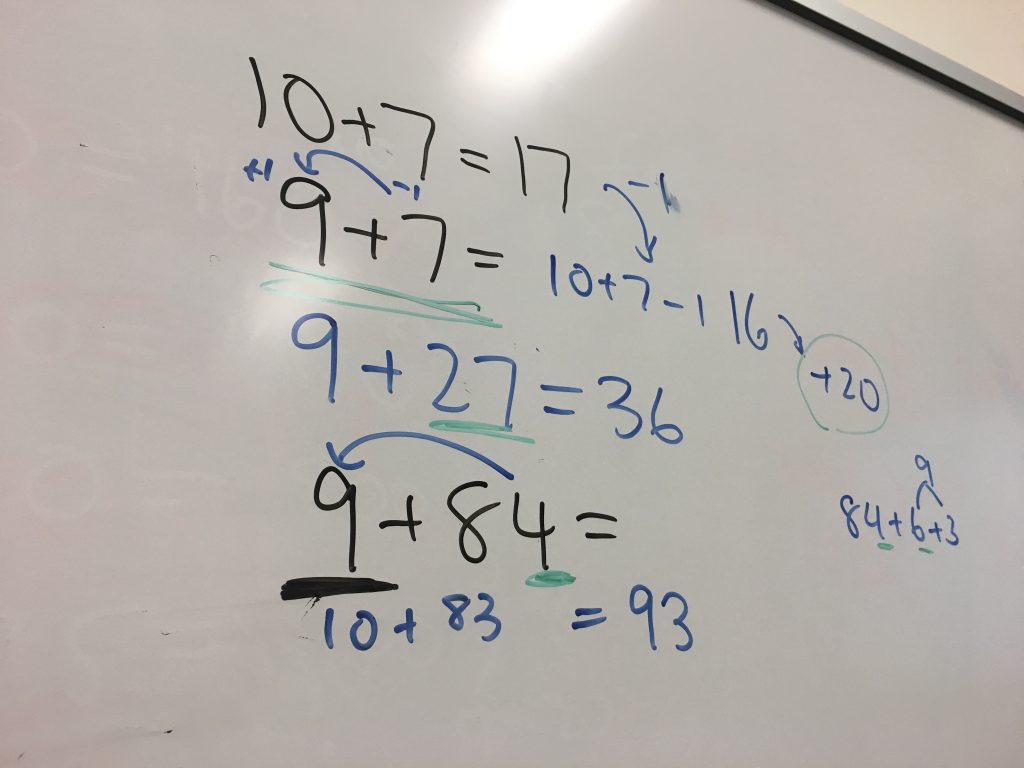A common concern that teachers often bring up is that their students solve number tasks mentally by ‘visualising’ the vertical algorithm. I’ve been asked a couple of times in the last month or so, How do I stop, or discourage my students from using a vertical algorithm? Or, How can I encourage my students to use methods other than the algorithm?
Algorithms are not innately bad
Before I delve too far into answering these questions in this blog, I think it’s important to mention that algorithms are not the ‘bad guy’, but they are also not the pinnacle strategy for our students to attain. The standard vertical algorithm is usually introduced when students are in middle to late primary school, often after other strategies have been introduced (such as; near doubles, bridging to ten, jump, split, compensation to name a few). This later introduction may be adding to the idea that it is therefore the ‘more efficient’ strategy. The vertical algorithm is a recording method, not a mental strategy. It is a way of recording, in short-hand almost, in a standard way (a convention) that others can understand. In essence it is probably more useful as a checking mechanism than as a working out strategy.
“Algorithms are introduced after students have gained a firm understanding of basic concepts, including place value, and have developed mental strategies for computing with two- and three-digit numbers.”
NSW Mathematics K-10 syllabus (page 36), NESA 2012
I think the above quote provides excellent advice to teachers about when to introduce students to algorithms. It is once they already have a variety of mental strategies already in place, and for quite large numbers. Introducing them earlier risks students losing their mental ability to computate. For students with limited place value knowledge, this may also lead to them become reliant on the ‘pen and paper’ procedure to solve even the most basic number tasks.
Russell (2000) talks about students who have the knowledge of procedures often try to simply remember the steps instead of trying to make sense of the problem through building on what they already know. These students are unable to choose the appropriate tools, only being able to use the procedure in the original context they were taught. This is one of the main reasons why learning a variety of mental strategies and flexible ways to partition, combine, regroup and rename numbers is our ultimate goal – so students can transfer this strategic knowledge into new and different situations.
“We believe that by encouraging students to use only one method (algorithmic) to solve problems, they lose some of their capacity for flexible and creative thought. They become less willing to attempt problems in alternative ways, and they become afraid to take risks. Furthermore, there is a high probability that the students will lose conceptual knowledge in the process of gaining procedural knowledge.”
Narode, R., Board, J. & Davenport, L. (1993). Algorithms supplant understanding: Case studies of primary students’ strategies for double-digit addition and subtraction (page 260)
So how do we encourage other strategies?
Students who have learned a procedure at the expense of previously known (or unknown) mental strategies now visualise the vertical algorithm when solving tasks. Our role is to assist them in re-creating (or creating) other visuals for the problems as well as creating a space where; the answer doesn’t matter, the algorithm will actually take longer, where the algorithm is no longer manageable to visualise, or where more flexible strategies come to mind quickly. I would also note here that you, as a teacher, may also visualise the vertical algorithm as this is ‘how you were taught’. I fit in that category and it takes practice and continual learning to ‘rewire’ your brain to work in more flexible ways to solve tasks. It was at university while studying my undergraduate degree that the mathematical pieces were put together for me and I was introduced to the wonderful world of alternate strategies. I now enjoy bringing these strategies to life for my pre-service teachers.
No.1 The answer doesn’t matter
For students who choose the algorithm as “a means to an end” and do not see value in finding other elegant ways to solve the task, just give them the answer. Whether it’s a word-based problem or a straight number equation provide these students with the answer and ask them to find ways to solve it. This shifts the focus to the processes needed. They may be required to share at least two strategies and can then use the algorithm to check, possibly with the inverse operation. It is also important that students can justify their strategy choice, not just that they can provide you with two ways to solve the task, but that they know which way is most efficient for that problem and why. You can also provide these students with a completed algorithm with an error and ask them to find the error and explain where the student may have gone wrong and what your advice would be to assist them in finding the correct solution. Theses types of questions are used in the NSW Department’s Stage 2 Diagnostic Assessment tasks.
No.2 The algorithm will take longer
To show students that their mental strategies can be much faster and more efficient than the algorithm will require you to be specific in your choice of numbers and equations you provide in class. Some suggestions include:
- Write a list of numbers horizontally where there are clear ‘combinations’ that are easier to add mentally than to write down vertically to add e.g. 12 + 18 + 13 + 17
- Use equations where compensation will be more efficient than applying a procedure that requires ‘borrowing’ or ‘trading’ e.g. 4017 – 3998 (this example is from DiBrienza and Shevell) or 301 – 299
- Add more than two numbers together so the students are encouraged to think differently e.g. 155 + 155 + 160
- Provide students with questions that link to ‘benchmark’ numbers or connect to other concepts e.g. 25 x 16 Knowing that 25 can be seen as a quarter (a quarter of 1600) makes this question easier to solve mentally than using a procedure
No.3 Creating other visuals than the vertical algorithm
The use of number lines, hundred charts, arrays and place value blocks to represent how to regroup and rename numbers can be useful models to help students visualise what’s happening to the numbers. Using the area model for two-digit by two-digit multiplication is also extremely helpful as the numbers produced link to the numbers within the algorithm. Note: At some point, when students are competent flexible users of number operations and have place value understanding, I would show them the connection between their mental strategies and the representation of these as a vertical algorithm. Up until this point, all of my questions/ equations are written horizontally (and would continue to be afterwards as well). This is particularly beneficial as students read the numbers left to right and aids in estimation and also in reading of large numbers.
No.4 Having other flexible strategies come to mind
The last dot point in No.2 above is a question that can be used as part of a Number String. Number Strings are similar to Number talks as they focus on students sharing mental strategies with the aim to build students’ ‘bank’ of computational strategies and make connections to mathematical representations. If we want students to choose to use strategies other than the vertical algorithm, we need to help them focus on the numbers in the problem and what they already know about them.
“A number string is a short (15-20-minute), daily routine in which a teacher presents a carefully designed sequence of problems one at a time for children to solve mentally. It is designed so that students develop a range of strategies for mental computation, explore the connections between strategies, and deepen understanding of such mathematical models as the number line.”
Lambert, R., Imm, K., & Williams, D. A. (2017). Number strings: Daily computational fluency (page 1)
We use number strings at the University of Sydney with our pre-service teachers (@janettebobis first introduced them to me as part of the Masters course she wrote). Using number strings in the classroom allows you to guide students to ‘see’ other ways to solve tasks in a specific way, e.g. using +10 then -1 for adding 9, using doubles and near doubles for adding, using doubling and halving for multiplication or using partial products for multiplication. Students are sharing their strategies while you as the teacher record their strategies (linking to visual models where necessary) and recording the connections students see between the string of questions, “how might they use this question to work out the next one?” For more on number strings, check out the links and references below.
To create your own strings you need to know your conceptual aim or strategy you are focusing on and I often ‘work backwards’ from the last, more complex, equation to create my string. For example, if I wanted students to use near doubles to solve a task the final question might be 35 + 38 … knowing that the question before that might be 35 + 37 … working back until my string looked like this:
30 + 30
32 + 30
32 + 35
35 + 35
35 + 37
35 + 38
Number strings focus on number patterns and relationships, it’s not about learning set strategies (like jump or split) but about learning when to choose them. When building students’ range of strategies we need to be careful that we don’t present mental strategies like jump and split to students without them having previously constructed similar strategies of their own. If we do, we risk them become pseudo-procedures (like algorithms) within themselves.
References
Clarke, D. M. (2005). Written algorithms in the primary years: Undoing the good work. Making mathematics vital, 93-98.
DiBrienza, J., & Shevell, G. (1998). Number strings: Developing computational efficiency in a constructivist classroom. The Constructivist, 13(2), 21-25.
Narode, R., Board, J. & Davenport, L. (1993). Algorithms supplant understanding: Case studies of primary students’ strategies for double-digit addition and subtraction. In J. R. Becker & B. J. Preece (Eds), Proceedings of the Fifteenth Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (Vol. 1, pp. 254–260). San Jose, CA: Center for Mathematics and Computer Science Education, San Jose State University.
Lambert, R., Imm, K., & Williams, D. A. (2017). Number strings: Daily computational fluency. Teaching Children Mathematics, 24(1), 48-55.
Russell, S. J. (2000). Developing Computational Fluency with Whole Numbers. Teaching Children Mathematics, 7(3), 154-158.
Teacher Education by Design https://tedd.org/number-strings/
Teaching Channel Number Strings example https://www.teachingchannel.org/video/multiplication-number-strings
Explore the #numberstrings or number strings search on Twitter