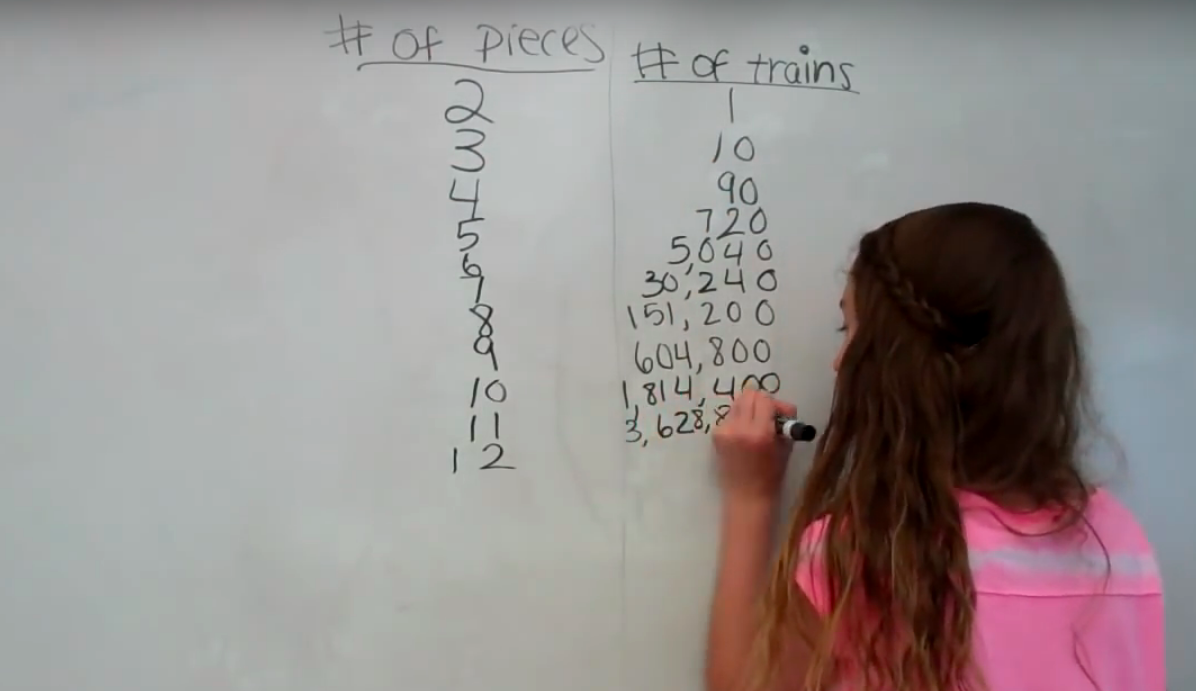Finding the right combination

Once again, a big-name company has brought mathematics to the masses- without even knowing it! Macdonald’s^® have their current offer on about choosing flavours for your frozen FANTA^® drink.

When I read the sign that you could make 36 different flavours, my brain went straight into maths-mode, keen to check their mathematics. Was that true? Is that the right number of combinations? How could this be represented? What if I could combine three flavours? These questions would make a great mathematics investigation for both primary and secondary students. My own kids were too busy eating their Macdonald’s to work it out, but it has so much potential for the classroom.

The problem has the parameter that you can have single flavours as well as combinations, so this may pose a complexity for students during their solution strategies. Also, some younger students may not realise that once you have say orange- raspberry, you can’t also count raspberry-orange (unless you want include this possibility, maybe you want orange on the bottom!).

Exploring combinations, permutations and combinatorics are all part of our NSW mathematics syllabus. Combinations (beyond number combinations) first appears in Stage 2 Chance 1 of the syllabus:

This concept isn’t specifically mentioned again until combinatorics within extension 1 in Stage 6. There are however aspects of finding combinations within probability and patterns and algebra that extends from Stage 2 through to Stage 5.

Even though there may not seem to be a clear thread of this content across the learning continuum, activities involving finding combinations or patterns are still important. Particularly, as representing these patterns through tree diagrams or tables or organised lists are all useful strategies within the working mathematically processes,  particularly problem solving.

These types of pattern activities may not be open-ended but fit into a more recently termed strategy, Open Middle^™ tasks, where there are multiple ways that students solve the task (open middle) and the end solution is still the same (closed end). Some other great examples tasks like this one are:

The handshake problem

This is a classic problem and is used regularly in many mathematics classrooms (see links to versions below). This is a nice task to introduce students to combinations and allows them to ‘act it out’ or ‘draw a diagram’ to make sense of the mathematics going on. You can adapt the problem to use a smaller number of people shaking hands or change the context, like the example to the right from the NSW Department’s Red Dragonfly Mathematics Challenge resource that uses ‘good mornings’.

All aboard train puzzle by Marc Boutavant

“Children will adore the imaginative art and quirky characters on both sides of each puzzle piece, making it possible to arrange the train in countless ways!” All aboard train puzzle

Countless ways you say?

Here’s another great resource to use in the classroom to explore patterns and permutations. This game lends itself to permutations as the order matters (the train has a front and end carriage) whereas for combinations, the order doesn’t matter. I was given a link to a great teacher video on solving the train puzzle problem How to arrange a train (A countable problem) which is well worth watching prior to trying out the task with your students.

Justin Solonynka uses the task with his Year 7 mathematics class and there is plenty of reasoning, problem solving and communicating involved. It works best if you have the puzzle itself as even though the pieces are doubled-sided, you can flip the whole train puzzle and find more combinations that way, but you can’t flip individual train carriages (as they no longer fit together.) Justin also made a follow up video using a different puzzle. Same students, different puzzle “we don’t think it’s actually countless” is their prediction for the new puzzle. It’s wonderful to see when students make connections from prior experiences to form new knowledge and apply this knowledge to new situations.

Remarkable animals by Tony Meeuwissen

This book was first introduced to me by @TregoningMich and what a remarkable book it is! It’s a flip book where you can interchange the head, body and tail of an animal to make a new creature with a new fantastical name. Apart from just the joy of making the different creatures, the descriptive text used for each animal also still makes sense when changed. This is done extremely well where for example, the first section of text ends with a noun and the second section begins with a verb (I’m sure @annettegray07 could explain this better from a literacy point of view!). In the classroom you could explore these patterns of language and allow students to create their own pages to add to the book. There is also mathematics to explore, the book states that you can make 1000 crazy creatures- this would make for a great investigation to explore the number of combinations of creatures.

I’m wondering how many ways could we explore these wonderful tasks?

Links

Red Dragonfly Mathematics Challenge ‘good mornings’ problem

https://www.nctm.org/Publications/Teaching-Children-Mathematics/Blog/Reflecting-on-the-Handshake-Problem/

https://nzmaths.co.nz/content/handshake-problem

Handshake problem https://nrich.maths.org/6708

Talking about patterns and algebra by NSW Department of Education

http://www.blake.com.au/v/vspfiles/downloadables/pt3_problemsolving.pdf

Friends and Strangers theorem https://www.youtube.com/watch?v=xdiL-ADRTxQ  by Numberphile

https://robertkaplinsky.com/the-difference-between-open-ended-and-open-middled-problems/

References

Sullivan, P., & Mousley, J. (2001). Thinking teaching: Seeing mathematics teachers as active decision makers. In Making sense of mathematics teacher education (pp. 147-163). Springer, Dordrecht.