Programming your practices
As the year draws to an end for most schools, planning for 2019 is beginning already. I thought it would be good to highlight some of the ‘buzz words’, concepts or ideas that are having an impact in mathematics classrooms.
When planning for mathematics at this time of the year, spend the time planning your practices not preparing your program. Good practices are what make good teachers. It’s not about activities, it’s about you! When planning for primary mathematics there are a number of pedagogical practices that you should have in your teacher toolbox, I’ve listed 6, but there are many more!
1. Noticing
The act of noticing is reflective of an inquisitive, curious mind. As teachers we want to foster these practices in students. One of the best ways to do this is by modelling. When you are a teacher who notices, students will start to mimic this behaviour. In mathematics things to notice include:
- similarities
- differences
- patterns
- connections to things we know
- errors
- change
Notice and Wonder about 7+5. #noticewonder #mtbos #iteachmath I love tilting the rekenrek to move all the beads... wish I could do the same with tens frames! pic.twitter.com/XyOdRHO0sK
— Berkeley Everett (@BerkeleyEverett) 20 November 2018
In mathematics noticing leads to learning and understanding of important aspect of mathematical concepts. Through noticing students are able to sort, classify, justify, reason, connect ideas, follow and reproduce patterns, predict and analyse mathematical information that is represented in a variety of ways.
Noticing is also a way for students to provide feedback to others about the effective strategies and various methods they use to solve problems. When students add comments to other students’ work, starting a sentence with “I noticed that you…” allows them to provide specific feedback based on the processes not the person.
“What math knowledge is needed for us to be able to notice mathematically important milestones in our students?”
Mark Chubb, Noticing and wondering a powerful tool for assessment
To be able to notice, you need mathematical content knowledge to know what you are looking for. Mark Chubb has a great blogpost that discusses Noticing and Wonder as these practices generally go hand in hand. I will specifically discuss wondering below but if you haven’t explored Noticing and Wondering yet, you can find our more by reading Annie Fetter, NCTM’s Math Forum , Kyle Pearce or exploring chapter 7 of Tracy Zager’s book, Becoming the math teacher you wish you’d had.
2. Wondering
Wondering is part of Noticing and Wondering, but they still have separate aspects to them and can serve different purposes. Noticing is the stage of the discussion that is often about observing and linking the visual representation to prior knowledge, whereas the wondering stage could be seen as the predicting and questioning stage- moving from the known to the unknown. This is an opportunity for students to pose problems to solve that often have the potential to lead to generalisations.
“…wondering helps them pose questions about what they have noticed. Rather than racing to find a solution, wondering allows them to slow down, to think, and do mathematics.”
Marie Hogan, Problem Solving—It has to begin with noticing and wondering
When using wondering as a pedagogy in mathematics it is important to undertake the noticing and wondering for yourself prior to the lesson. This is part of the lesson preparation where you can start to see the conceptual links and predict where students may take the lesson. Be aware though, this doesn’t mean you negate the wonderings the students have. It is important to see their ‘wonderings’ through even if they may take you on a teaching tangent as they may uncover misconceptions or misunderstandings. Embracing students’ wonderings also allows them to make connections across concepts. The purpose of pre-wondering for yourself, is to build you own practice of wondering and to build your own content knowledge.
Teaching talk the first week of school with #noticewonder. pic.twitter.com/V8eqEzq5NQ
— Kassia Wedekind (@kassiaowedekind) 31 August 2017
3. Connecting
“Making connections is at the heart of doing mathematics.”
Arthur Hyde, Comprehending math: Adapting reading strategies to teach mathematics, K-6
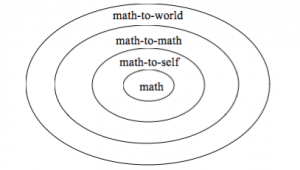
When planning for mathematics your first thoughts should be about what connections can I make? and what connections should I make? Many primary teachers are starting to use the reading comprehension connections ideas in mathematics, as discussed here. For young students, where possible, it is good to make connections to the students’ prior experiences (math to world). Making connections between concepts (math to math) is also essential when building the foundational blocks of mathematics for example, the links between area and multiplication (for more examples see my earlier blog). Then finding ways to hook students in to mathematics by highlighting its use and personal application (math to self), exploring ways that mathematics can be utilised in a range of situations.
4. Talking
“…five- to fifteen-minute conversations around purposefully crafted computation problems, are a productive tool that can be incorporated into classroom instruction to combine the essential processes and habits of mind of doing math.”
Sherry Parrish, Number talks build numerical reasoning
Whether its Number talks, Talk moves or Intentional talk classroom discourse is definitely at the forefront in mathematics education right now. The 5 practices for orchestrating productive mathematics discussions also provides clear guidance to teachers about what to focus on during classroom discussions:
- Anticipating students’ solutions to a mathematics task
- Monitoring students’ in-class, “real-time” work on the task
- Selecting approaches and students to share them
- Sequencing students’ presentations purposefully
- Connecting students’ approaches and the underlying mathematics
5. Justifying
Justifying is synonymous with reasoning which is one of the NSW mathematics K-6 syllabus working mathematically processes that sit at the heart of the syllabus. Students’ abilities to justify can be developed and enhanced through the way we question in the classroom and the kinds of tasks we ask students to complete.
To be able to justify, there needs to be a statement to defend or rebuff. Providing students with questions that rely on a True/False response provide opportunities for justification of thinking. As do providing non-examples or incorrect solutions where students need to find the errors or justify which answer is correct and why.
“Research emphasizes the benefits of incorrect examples, especially as a means of illustrating misconceptions.”
Durkin & Shafto, 2016
6. Prompting
The use of enabling and extending prompts in the mathematics classroom open tasks up by creating a low floor (access point for all students) and high ceiling (further application point) for students. Peter Sullivan’s book Challenging mathematics tasks includes enabling and extending prompts to engage all learners with the tasks. The reSolve: maths by inquiry project tasks also include these prompts.
“Posing questions with multiple entry and exit points
Such tasks :– are simply posed drawing on content with which the students are familiar (although the connections may be new)
– can be responded to in both simple and complex ways, with responses of all students being potentially of interest
– are easily accessible (so everyone can start) but have potential for sophisticated responses (and so can challenge those who can to go further)”
“Posing challenging tasks supplemented with enabling and extending prompts
Such tasks:– are set at levels that provide reasonable challenge for all students
– include an expectation that students will communicate their responses clearly in writing and verbally
The prompts:
– connect directly to the original task
– allow all student to contribute to task reviews”
All of these practices revolve around the concept of communicating.
- teacher to student (what mathematicians do)
- student to teacher (what I think, what I know, what I want to know)
- student to student (talking like mathematicians)
They are research and/or classroom-evidence based. They are not about individual activities mapped to content but about teaching intent, teaching purpose, and teaching practice. Focus your planning on how you teach, then you will be able to read the syllabus, identify what learning your students need, and teach.
References
Durkin, K., & Shafto, P. (2016). Epistemic trust and education: effects of informant reliability on student learning of decimal concepts. Child development, 87(1), 154-164.
Hyde, A. A. (2006). Comprehending math: Adapting reading strategies to teach mathematics, K-6. Portsmouth, NH: Heinemann.
Talk moves: A repertoire of practices for productive classroom dialogue
3 Strategies for Bringing Argument and Critique into Common Core Math Classes








