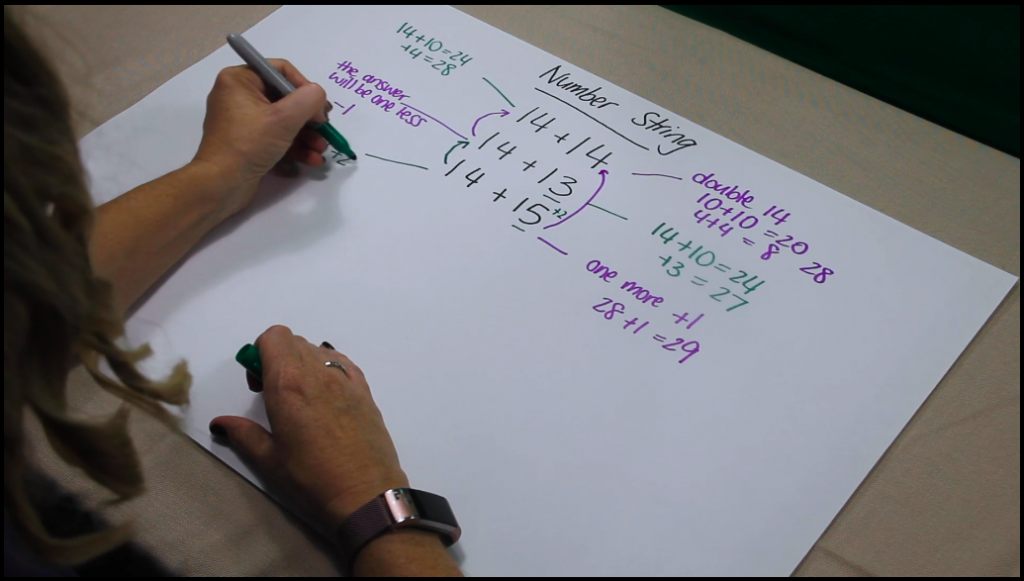In a time when everything is being home delivered, I thought I’d take this opportunity to remind teachers of the online courses we have available through our website. Annette just launched her first course Talking about Learning and wrote about it in her blog from a few weeks ago. I have written 10 courses about unpacking numeracy. They highlight different elements of ACARA’s National Numeracy Learning Progression as areas of focus for students’ point of need. Even if you are not using the progression, these courses are a great introduction to aspects of numeracy that are essential for student development. Each course has a pre-reading of related research and provides; common misconceptions, concept explanations, teaching techniques and learning experience ideas and links. My blog this week gives a taster of some of the content from the courses.
Talking about interpreting fractions
There are numerous concepts within fractions that students need to become familiar with along with different models of fractions. Fractions as; part-whole, measure, number, quotient and ratio are the main models presented to students during primary and early secondary school. Students also need to be able to identify and create fractions in discrete and continuous representations. The talking about fractions course highlights these models and provides teaching ideas to support fraction development.
Talking about quantifying numbers
Within the quantifying numbers course I share several teaching strategies that have emerged in the last few years that assist students in understanding how to quantify numbers. Steve Wyborney’s (@SteveWyborney) Esti-Mysteries focus on students developing estimation skills related to large and small quantities is an excellent example. Along with Steve’s work, I also talk about Choral Counting and Counting Collections. This book by Franke (@meganlfranke), Kazemi (@ekazemi) and Turrou (@Angelaturrou) was a ‘game changer’ for me in how to talk with students about numbers, big numbers, and the patterning structure of place value.
Talking about operating with decimals
Understanding decimals is often just as hard for adults as it is for students. Many misconceptions surround this concept and these misconceptions are well-researched and documented by researchers such as Kaye Stacey and Vicki Steinle. In their paper, A longitudinal study of students’ understanding of decimal notation: An overview and refined results common misconceptions are explored. Along with Stacey and Steinle’s paper, Peter Gould’s paper Preventable errors: From little things, big things can grow was utilised in the course as stimulus to discuss these issues.
Peter talks about the need for students to have benchmark fractions and their related decimals as a knowledge base. I also used this student work sample image to talk about the importance of what it means to know something, like one-half, as highlighted by Gould. Students need to know what is one-half, but also what isn’t one-half.
Talking about operating with percentages
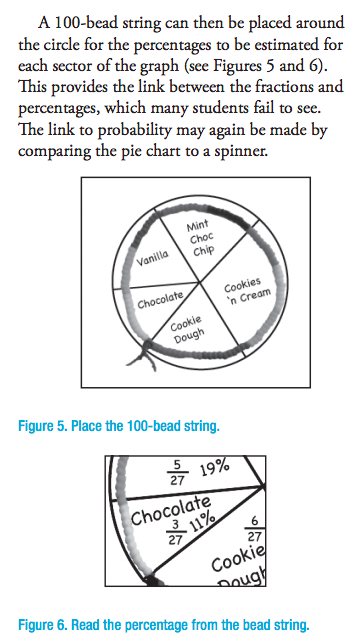
Each course also provides teachers with links to websites and research referenced within the course that relates to the topic. For Talking about operating with percentages, one of the additional research readings I recommend to teachers is Purposeful Statistical Investigations by Lorraine Day (@BUBBLINGDAY). This is an excellent paper written for the APMC (Australian Primary Mathematics classroom) journal. Day explores various classroom activities with students concerned with data investigations and exploration using various resources. One resource she uses is bead strings, linked to creating sector graphs and applying knowledge of percentages. Day makes clear the connections between concrete and abstract representations to explain the junction of fractions and percentages as mathematical concepts. The AAMT (Australian Association of Mathematics Teachers) produces the APMC journal. I highly recommend this journal for primary classroom teachers. You can access the journal through membership of your state’s mathematics association – in NSW it’s MANSW, in Victoria it’s MAV, in WA it’s MAWA, in SA it’s MASA, in TAS it’s MAT, in Canberra it’s CMA, in NT it’s MTANT, In Queensland it’s QAMT.
Talking about understanding units of measurement
In my courses I like to use images that could be used in the classroom as part of Notice and Wondering conversations with students. If you complete the course with other teachers, you can pause the videos and discuss the images with your colleagues. My first series of courses were initially run as live webinars and recorded, so there are many opportunities to discuss the concepts with others or take part in some self-reflection.
This image of a duck was a Noticing and Wondering starting point for the course on understanding units of measurement. I have also created a number of PowerPoint presentations with images that teachers can use for Notice and Wonder conversations, they are available freely on our resources page, just search for ‘noticing’.
Talking about additive strategies
Within the Additive strategies course, I talk about different methods students develop to solve addition and subtraction problems. To assist students to making decisions about when to apply what strategies I also share teaching strategies such as Number Talks and Number Strings (see image below from the number strings video). It is important that students have opportunities to talk about their thinking and also provide reasons why they think their strategy will work for a problem or why perhaps there is a more efficient strategy. Part of developing these skills involves using prior knowledge about addition and subtract to help – moving from the known to the unknown.
Talking about multiplicative strategies
When it comes to talking about multiplicative strategies there is plenty of recent research (see references below) and teaching strategy resources available particularly at the point where students shift from using additive to multiplicative strategies (usually in middle years). One researcher that has lots of offer on this concept is Dianne Siemon. The paper that Siemon and Breed wrote titled Assessing multiplicative thinking through rich tasks describes tasks they used to identify if students were using additive or multiplicative thinking. Their work along with the research of others such as Hurst and Hurrell provide teachers with clarity around what we are looking for when we talk about multiplicative thinking.
“… while most students are able to solve multiplication problems involving relatively small whole numbers, they rely on additive strategies to solve more complex multiplicative problems involving larger whole numbers …”
Siemon & Breed, (2006) Assessing multiplicative thinking using rich tasks
“The transition from additive to multiplicative thinking is one of the major barriers to learning mathematics in the middle years.”
Siemon, Breed, & Virgona, (2005) From additive to multiplicative thinking – the big challenge of the middle years
“Multiplicative thinking … underpins important mathematical concepts such as fraction understanding, proportional reasoning, and algebraic thinking.”
Hurst & Hurrell (2016) Multiplicative thinking: Much more than knowing multiplication facts and procedures
Talking about number patterns and algebraic thinking
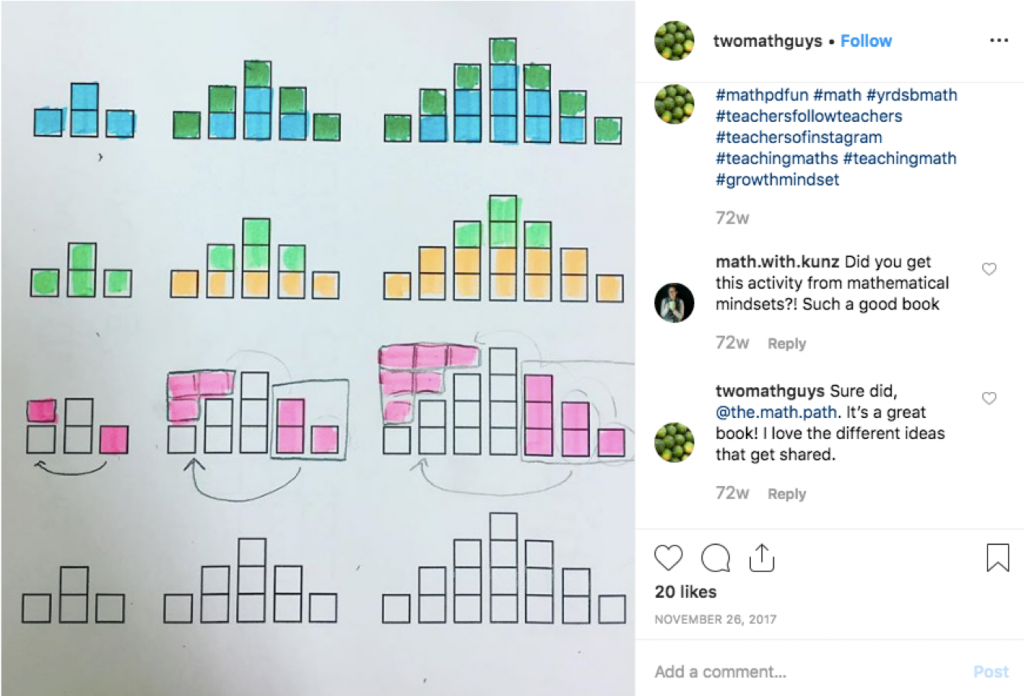
In Talking about number patterns and algebraic thinking, I use a growing patterns task Squares upon Squares from youcubed. It is a lovely introduction for students in middle to upper primary to growing patterns and exploring visually what is happening. On the task outline there is a reminder for teachers about the importance of first working visually prior to numerically: “… we ask that they [students] make their answer entirely visual, that they forget about counting and numbers. Color coding is often a great tool for this.” I also reference this Instagram post by Twomathguys that shows some solutions visually.
Talking about comparing units
As part of engaging in each course there are quiz questions to complete within some chapters of the courses. These are sometimes mathematics questions related to the concept being discussed, like this quiz question that’s part of Talking about comparing units. The quiz questions provide time for teachers to think through the concepts and how they, or their students, may tackle the mathematical problem provided. In the case of comparing units, an ability to solve problems involving rates or ratios is heavily reliant on students having an understanding of proportional reasoning.
Talking about representing and interpreting data
In exploring the sub elements of the numeracy progression, it was important to make connections to the research from which the progression levels were drawn, or to research that relate to the numeracy concept. In this case, levels of the sub element Interpreting and representing data describe statistical literacy skills that students need to demonstrate. These skills, such as the four roles of the statistical text user by Watson and Callingham (2003), are described in detail within the course and ideas of what this might look like in the classroom are shared.
Each course is 2 hours in length and provides registered hours for accreditation through NESA for NSW teachers. You can register for the courses via our Learning Management System heroica. We hope that these online courses might be beneficial and a way to access PL for teachers, especially at this time when face-to-face PL may not be available.
References
Day, L. (2014). Purposeful statistical investigations. Australian Primary Mathematics Classroom, 19(3).
Gould, P. (2017). Preventable errors: From little things, big things can grow. Australian Mathematics Teacher, The, 73(4), 29.
Hurst, C., & Hurrell, D. (2016). Multiplicative thinking: Much more than knowing multiplication facts and procedures. Australian Primary Mathematics Classroom, 21(1), 34.
Siemon, D., & Breed, M. (2006). Assessing multiplicative thinking using rich tasks. In Annual Conference of the Australian Association for Research in Education.
Siemon, D., Breed, M., & Virgona, J. (2005). From additive to multiplicative thinking–the big challenge of the middle years. In Mathematics: celebrating achievement. Proceedings of the annual conference of the mathematical association of Victoria, Melbourne: MAV.
Steinle, V. & Stacey, K. (2004). A longitudinal study of students’ understanding of decimal notation: An overview and refined results. In I. Putt, R. Farragher & M. MacLean (Eds.), Mathematics Education for the third millennium: towards 2010. Proceedings of the 27th annual conference of the Mathematics Education Research Group of Australasia (pp. 541‐548).Townsville: MERGA.
Watson, J., & Callingham, R. (2003). Statistical literacy: A complex hierarchical construct. Statistics Education Research Journal, 2(2), 3-46.