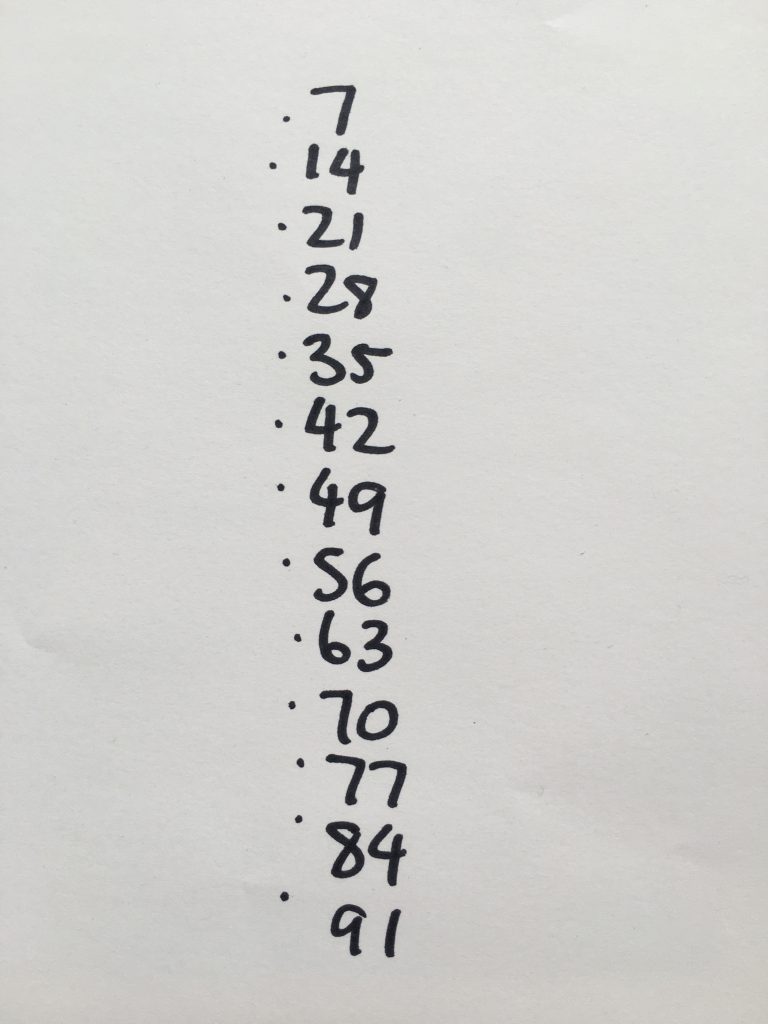“If they just knew their times tables”

I would like to first say that I do not like the term ‘times tables’. I think for many, it brings up connotations of sitting at school learning facts by rote often under the pressure of time. Whether this was a positive or anxiety-inducing experience, neither assists students in making the connection to the process of multiplication. Our Australian Curriculum refers to ‘multiplication facts’ and ‘number sequences’, no where does it mention the wording ‘times tables’. The facts themselves are not ‘tables’, they can be displayed in a table. If you want to refer to the table structure used to display multiplication facts – the better, or more appropriate term, would be ‘multiplication table‘ as it is formally known. Or, talk with students about learning multiples.

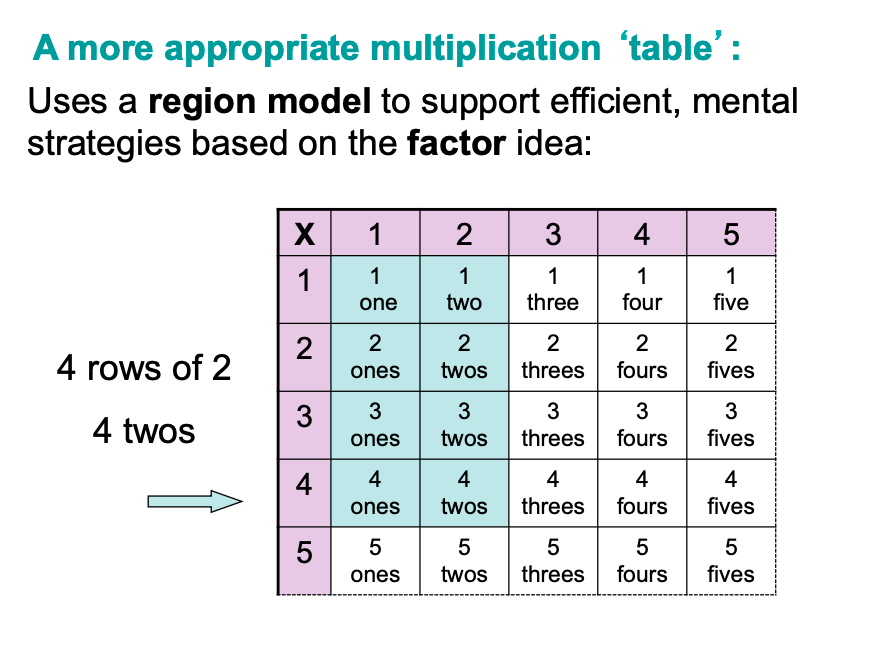
I will set out my discussion of how, when, and why to learn multiples (conceptual understanding, not rote memorisation) under the following headings:

There’s not 144 facts

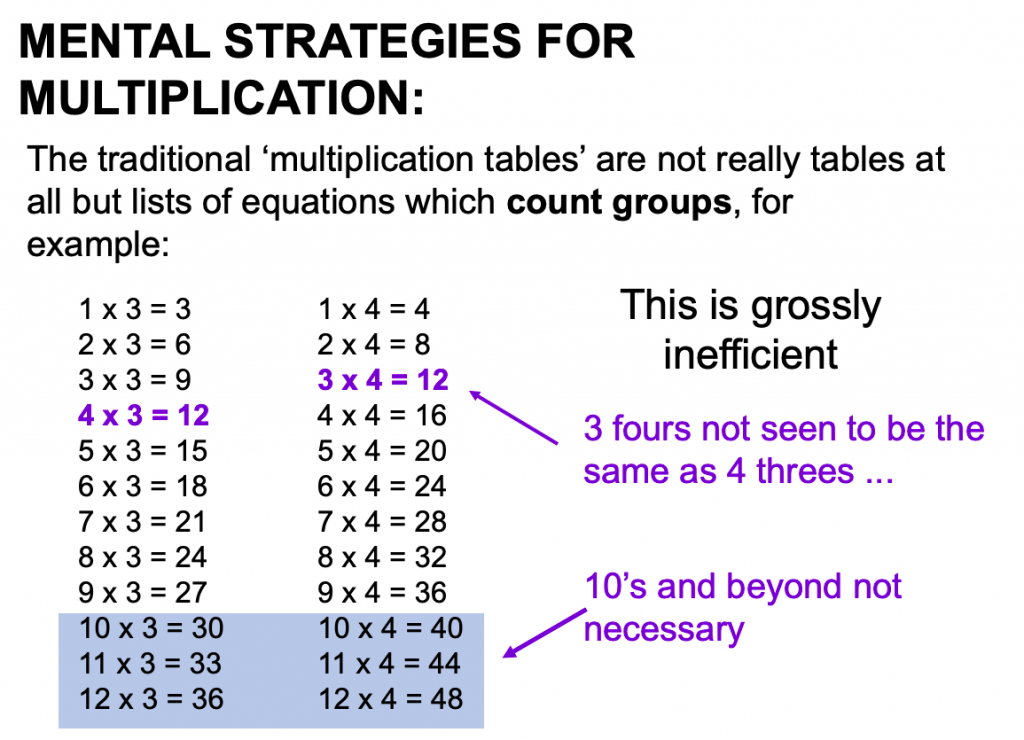
Learning multiples is part of building ‘basic facts’ that are the foundation for operating with numbers. Knowledge of multiples though, does not equate to seeing them as a set of facts to memorise. However, the way they have often been taught in the past (or the times tables practice books or posters used) does just that. It might not have been the intention of the teacher, but students think multiples stop at 12. I recall teaching a lesson in a Grade Three class and asking students a question related to 13 x 10. One student immediately put up his hand and said “you can’t do that, times tables only go to 12”. The problem with learning a set of facts, is that if how they should be used or why they are the basis for building more facts isn’t clearly articulated to students, then the connections are not made.

Slide 34 from Dianne Siemon’s presentation The key ideas and strategies that underpin Multiplicative Thinking (accessed via Education Victoria)

Learning multiples from 1 x 1 = 1, 1 x 2 = 2, 1 x 3 = 3 onwards to … 1 x 12 = 12, suggests to students that there are 144 facts they need to remember. There is not 144 facts, as once you have an understanding for example of 3 x 6, then you know 6 x 3. This relationship between certain multiples will be discussed further below. In NSW, our syllabus document hasn’t stated “up to 12 x 12” for at least 30 years due to our use of the metric system and base ten. This is not to say that learning multiples beyond 10 x 10 isn’t beneficial. Multiples of 11 are a great pattern, and learning how multiples of 12 can be solved by using place value knowledge of 12 as 10 + 2, to then work out 12 x 8 by doing 10 x 8 then 2 x 8 and adding the total is developing great mental strategies.

Automaticity does not equate to rote memorisation

When teachers say they want students to know their ‘times tables’, what they may be referring to is that they want students to be able to recall basic facts and draw upon prior knowledge when solving more complex tasks. Drawing on known facts is part of automaticity, it’s that point you get to where you ‘just know’ that 2 fours are eight. You don’t having to think deeply or use your working memory to ‘work it out’ – you just know. Automaticity is important and is still a goal of mathematical thinking. However, wanting the result of teaching multiplication to be that students readily recall knowledge of multiples (within an appropriate period of time, not having to count by ones to solve 2 x 4), does not mean the process by which they learn multiples should be about readily recalling – i.e. rote memorisation.

I think about it in the same way as being efficient, or for want of a better word, fast, at swimming. To become a champion swimmer, the end goal is to be the fastest. But to become the fastest, your coach doesn’t tell you to jump in and swim as fast as you can. The coach helps you develop different skills at different times – stroke, turns, breathing. Then, as these skills develop, the pace is introduced. This is a good analogy for how students should be learning multiples. To have ready recall of facts, I don’t teach them at speed or ask students to write or practice them as lists as rote memorisation. I want to build smaller skills that connect to understanding multiplication as a big idea. Then the fluency, accuracy and automaticity will develop alongside the understanding. Recall is the result, not the process.

Multiples that students are learning, need to relate to the whole multiplication concept – just like understanding how tumbling turning makes you a more efficient swimmer overall is important, where tumble turns are not the end product themselves. You can see when students have learnt multiples in isolation to their conceptual understanding by how they solve multiplication and division task.

From Grade 3 onwards, if you look at students’ working out (it may be hidden on another page, on scrap paper, or has been rubbed out) to solve 7 x 13, and you see either of the two examples I’ve drawn here. Then the student is not using efficient mental or written strategies for multiplication. They may even ‘know’ the ‘times tables’ but do not see how they connect to solving the task at hand. Or they have learnt them ‘in order’ and are only able to recall them in a set order to use them.

Learning ‘times tables’ by rote or in order, can be counterproductive to developing understanding. As mentioned above, they may not see that 3 x 6 is the same fact as 6 x 3 when they learn them separately and are therefore unable to use previously learned facts to solve unknown facts. For the 7 x 13 question, students need to draw on prior knowledge of either 7 or 13. There are more ways to solve this question than the two strategies I’m sharing here, but these are two efficient ways students should be able to use mentally. If they know that 13 is 10 + 3, then they can use knowledge of multiples of 10 and 3. If they don’t know multiples of seven (which by the way are the hardest facts as seven is not double any smaller known facts) they can start with, “I know multiples of 5” and “I know multiples of 2” knowing both of these smaller facts will assist them in working out 7 x 13.

These strategies are more efficient than going back to one seven, then adding on 13 sevens, or going through a list of multiples of seven. The earlier we develop these flexible strategies the better, so they become students’ ‘go-to’ strategies. When the numbers get more complex or when division questions arise like 372 ÷ 6, I do not want my students counting by sixes to solve this task.

But they need to know them later

This statement is true, students do need to have recall of multiples for more complex mathematics like solving division task, working out equivalent fractions, simplifying fractions, multiplying fractions and/or decimals, inverse operations, solving order of operations questions, finding equivalent ratios, and solving rates problems to name a few. However, if students do not know multiples at speed, as long as they have an efficient strategy to work the multiplication out, they will still be able to solve more complex problems. What they need to build is connections between multiples, using a range of alternate strategies instead of counting by multiples from the first multiple e.g. 1 x 7 to solve questions. One of the first ways to do this, is to help students start to use what they already know.

This may seem obvious, but to young children it isn’t. Take for example the number 16. I have a number sense assessment that uses the number 16, and one of the questions relates to making an array with 16 tiles: How could I divide 16 tiles into equal rows? Most students make a four x four array first. I then ask, is there another way to put the tiles in equal rows? Many students start to guess, 1, 2, 3, 5, in each row? They try these ideas out as using trial and error with the tiles, some work and others do not. A student with well-developed conceptual skills related to multiples would straight away rule out 5. Students who understand multiples, should immediately be able to say “It can’t be 5 in each row, as 16 is not a multiple of 5″. Or they might say, I could try 2 in each row, because 16 is an even number that can be counted by twos”. These are higher order thinking skills in relation to multiples – but this is what we are looking for when we think about being proficient in mathematics, or for students to be working mathematically. This type of thinking does not come from rote learning multiples, it comes from understanding the concept of multiplication.

Helping students using the multiplication table: Teaching relationships not recipes

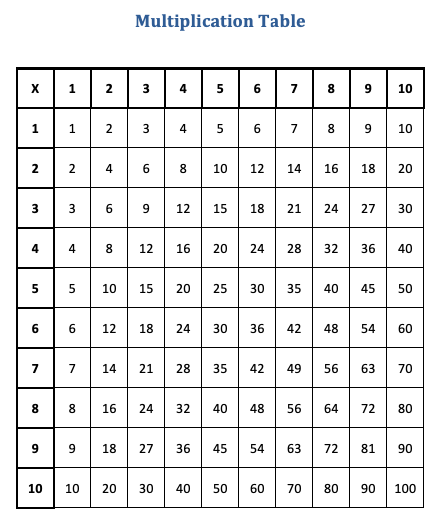
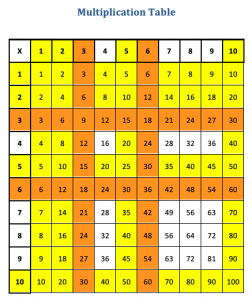
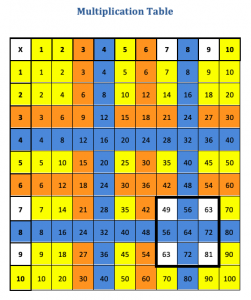
The multiplication table is a great resource to help students learn multiples. I will also add here, that if you are a parent or carer, there is no harm in helping your child by practicing multiples at home. It may be a different focus to how we teach them in class, but consolidating knowledge built conceptually at school, with practice at home, is always beneficial. Once students start learning about multiples of 1, 2, 5, and 10, the table becomes a visual way for students to ‘see’ the starting multiples up to 10 x 10. Seeing how they are related, and keeping track of what they already know. Every student should have one printed out and in their mathematics work book or readily available on their desk. I’m not concerned with if they can see the ‘answers’, my focus is on learning how they relate and looking for patterns and efficient strategies to work out other multiples.

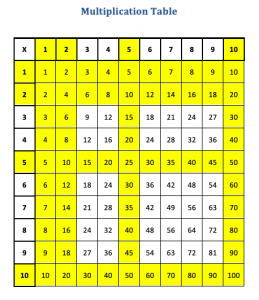
The next step is having students identify what they already know. This is an ongoing process and can be repeated throughout the year, and over the primary grades. You could also use an empty table and have students add in the multiples as they gain confidence in using them appropriately. Generally, students begin by highlighting multiples of 1, 2, 5 and 10. They may need guidance to see that they can highlight both the vertical and the horizontal column. Then, students may start to develop confidence with multiples of 3. This is then a point where teaching instruction needs to build on the concept of doubling (and halving). That is, if I know my multiples of 3, I can work out my multiples of 6 and vice versa. Then, the same process can happen with the multiples of 4 and 8.

This process also reflects how we introduce fractions and their related fractions (fifths and tenths, thirds and sixths). After these multiples are developed, only a small number of ‘facts’ remain. The nines can be seen as one less than 10, or learned through the consecutive number pattern both the ‘tens’ and ‘ones’ numbers create. As previously stated, the sevens can be difficult as normal halving and doubling strategies are not always fruitful. But this reduces the focus to only a small number of facts that require more focus than others. Knowing that 7 eights are one of the more difficult multiples for students to learn, I made a game to assist students (it can be adapted to other multiples).

Professor Dianne Siemon from RMIT has conducted research into multiplicative thinking and works with teachers to develop quality teaching practices to support the development of multiplicative thinking in students. Many of her resources are available online, such as this PDF of one of her presentations which is a fantastic resource. In the presentation, Dianne shares visuals that support the development of multiples. This resource from the NSW Department of Education also provides excellent ideas and strategies to support the development of multiplicative thinking.

Other useful visuals

Then what do we do as teachers if we don’t just practice ‘times tables’? We use visuals. I’ve already shown the use of the multiplication table. Another great resource is the array structure of multiples. I use arrays of dots as flash cards to build automaticity with multiples.  At first students may try to count the dots by ones, this will work for smaller multiples but eventually they will see a need to use other strategies. Strategies such as looking across and down to work out ‘how many’ rows and ‘how much’ in each row, then using mental strategies to work it out. Students start to notice the row across and down, still understanding the count includes the ones in the middle. If they think it’s approximately 4 across and 6 down, their answers should be 24 or at least 20 or 25 – that would be plausible close multiples. The array visuals also support the development of concepts of area and highlight square numbers as making ‘squares’.

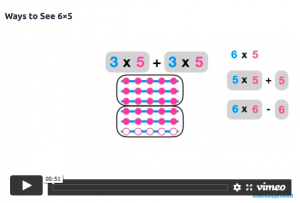
Berkley Everett (@BerkeleyEverett) who makes fantastic visuals available on his MathVisuals site has a range of vimeo videos that show how multiplication works. These are great to show students (and teachers) that highlight the action of multiplying. The dynamic nature of some abstract concepts are often hard to show with concrete materials so these videos provide the link between the visual and the numerical representations.

Using a multiplication grid that shows the ‘real’ scale of multiples is another helpful resource for students. There are a few of these around online. This version by The ChalkFace would be my recommendation. Others have made nice interactive versions too, as shown in this tweet. The scaling assists students in seeing how the multiples increase and show the relationship between multiples like 2 x 8 and 8 x 2 where the commutative property can be noticed visually to support the numerical representation.

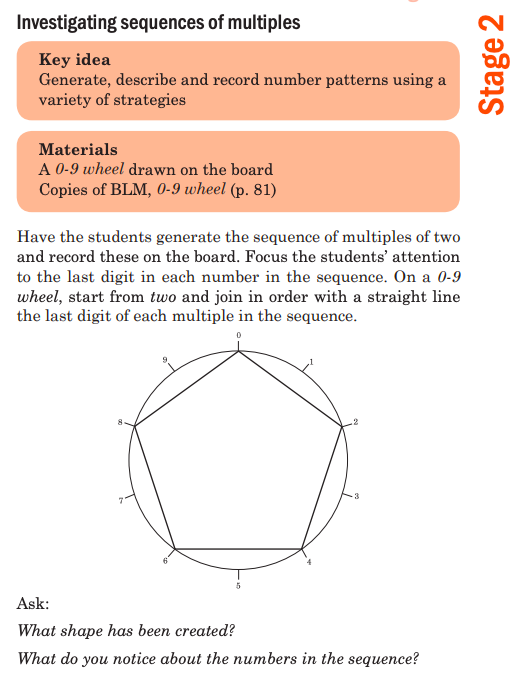
Visuals that focus on the patterning nature of multiples can be explored with students as well. The NSW Department of Education’s Talking about Patterns and Algebra resource has plenty of ideas to guide this process. I particularly like the pattern wheels (pictured). The resource does not map to current NSW syllabus outcomes but the tasks are still useful and high quality. I also like this investigation of the patterns in multiples on the Multiplication Table entry on Wikipedia.

Creating thinkers not calculators

Education has changed over the years, and teachers are great at innovating and adapting to meet the needs of both their students, and the world into which they will live. Technological advances means that students need to be problem solvers, problem finders, and be flexible knowledge holders – not regurgitators of knowledge. Our job as mathematics educators is to create thinkers, not calculators. The basics are important, but they are just that, basic. Multiples are a starting place from which to jump forward into the wonderful world of mathematical thinking. I was reading an article The Multiplication Table: To Be Memorized or Mastered? by John Trivett from 1980 as I prepared this blog. Although the article is older now, his words of wisdom about the place of the multiplication table in learning multiples, I believe, is still relevant today:

References

Trivett, J. (1980). The multiplication table: To be memorized or mastered?. For the Learning of Mathematics, 1(1), 21-25.