A few weeks ago I shared a tweet about arrays after discovering a great website (sineofthetimes.org) by Daniel Scher (@dpscher). I really appreciated the dynamic application he had created using Web Sketchpad to make and explore arrays. It’s quite simple in its design but I think that’s the beauty of it – no additional distractions on the page to shift the focus of students away from the mathematics. Once I played with making some arrays and non-arrays, it got me wondering. Could we help students build multiplicative relationships using benchmark arrays?
First, I should probably explain what I mean by examples and non-examples of arrays. To me, this is just showing how I can make a ‘correct’ array for say 12 where there are three rows of four. Then I might want to show how if I tried to make equal rows of 5, it wouldn’t work. I’d get two rows of five and a partially filled next row of two. The latter is what I would call a non-array, pretty much just division with remainders.
I often find students in Grade 3 onwards struggle to visualise what remainders are. As a teacher, you may see this struggle or lack of understanding later in Grade 5 or 6 when trying to explain to students how to represent remainders as fractions – they don’t know which number to use as a denominator. So I feel that if students had a better visual of remainders earlier, that show what they are (i.e., the beginning of the next row or multiple group), students may understand how 12 ÷ 5 = 2 r2 is the same as 2 and 2/5. This understanding also connects to the relationship; 12 ÷ 5 as the same as 12/5 (12 fifths).
Loving exploring arrays using this neat app on https://t.co/efnnpTE8DA @dpscher thank you so much for your amazing site! Hadn’t seen it until recently! I love that you can make examples and non examples of arrays. pic.twitter.com/G3YgduD6QV
— katherin cartwright (@kath_cartwright) November 7, 2021
Second, I should probably elaborate on my thinking about benchmark arrays. Benchmarks in mathematics are often referred to when students work out problems using known quantities as comparisons, e.g., in fractions. Clarke and Roche (2009) talk about students using benchmarks to compare fractions, such as comparing other fractions to 1/2 or to the whole to work out their size or order. Post et al., (1986) phrased this type of strategy as transitive, where students make use of known external values. Benchmarks also exist in measurement concepts such as 1 kg in Mass and 1 Litre in volume as a reference point for comparisons. Hence my wondering about if students might benefit from having benchmark arrays as a visual starting point to work out or estimate other quantities.
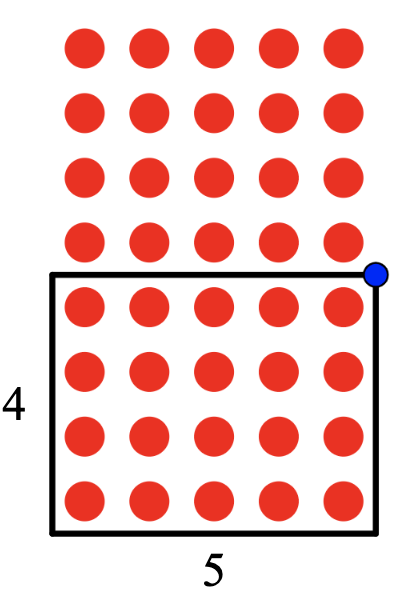
So, I used Daniel’s array maker to think about how students might be able to work with some benchmark arrays, developing these images as a starting point to compare to other quantities. The two numbers I thought might be most helpful would be a 2 x 5 array, the representation students are most familiar with as a ten frame. The other being a 4 x 5 array of 20. In my classroom I always had containers of counters for students to access when needed. The first job when using the counters was to make a 4 x 5 array to check they had the right amount! Below are some images I created using Daniel’s site where these benchmarks might come in handy.
When looking at the 8 rows of 4, students might notice the 4 x 5 array within the larger array and see that they could double it. This strategy is a nice way to use known facts to solve unknown multiples. The second array of 5 x 5, they might see a ‘ten frame’ 2 x 5 array and see they can make it at least 2 times, so the number will be larger than 20, with one more row of 5 it wold be 25. For the 5 x 5 they may also see the 4 x 5 array and use that.
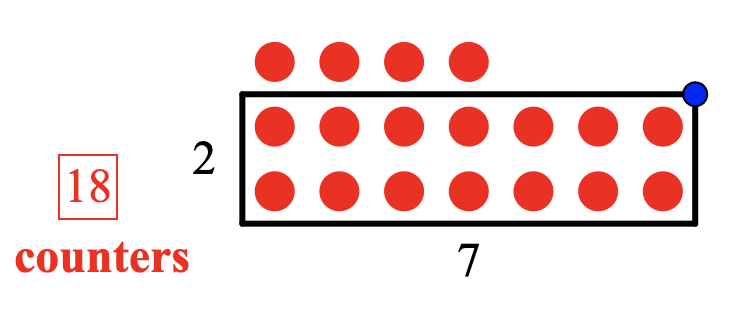
You can also use the array creator to set a number of counters, in this case 18 and ask students to make a non-array with the largest remainder. In the image here I have made a 2 x 7 array with a remainder of 4. I wonder could you make a different array with a larger remainder? If you can, how do you know there are no other options? You could also play this off computer and just turn over 2 cards to make a 2-digit number (maybe just cards 1-5 to start with).
This game would be great to play with Grade 3-6 students. It’s similar to a game we had as a learning object at the NSW Department of Education called Remainders Count, it was part of the Count Me In Too project. I liked it as the aim of the game was to make the largest remainder, assisting students to think about the number closest to the next multiple. You can no longer use the interactive game, but this document about the learning objects includes how to play the game offline (see p. 15).
Well, I’d love for any teachers to try out my idea about arrays as benchmarks for estimating larger quantities. Maybe I could challenge Michael Minas (@mminas8) to make up a game about array benchmarks or play my arrays game with Nash!?
References
Clarke, D. M., & Roche, A. (2009). Students’ fraction comparison strategies as a window into robust understanding and possible pointers for instruction. Educational Studies in Mathematics, 72(1), 127-138.
Post, T., Behr, M. J., & Lesh, R. (1986). Research-based observations about children’s learning of rational number concepts. Focus on Learning Problems in Mathematics, 8(1), 39–48.