When teaching writing to our students we provide time for planning. When teaching writing to our students we also allow for drafting and re-drafting of ideas, paragraphs, and plot lines. How often do we allow students to revise their thinking or work in mathematics? How often do we allow students a second or third revision of a mathematical problem? How often do we publish their final draft and display it in our rooms, the way we may do with a piece of writing? These are questions I ask myself, and the teachers I work with, and it seems I’m not the only one.
“Rough-draft talk is talking to learn.”
Jansen, Cooper, Vascellaro and Wandless
I recently stumbled across Amanda Jansen @MandyMathEd and her hashtag #RoughDraftMath and was excited to hear that there is a movement towards rough-draft talking in mathematics where students can feel free to share ideas as part of an on-going thinking process, not just as a final draft. This along with other pedagogical practices such as Talk Moves, Number Talks and Gallery Walks are researched ideas leading the way to a new norm in mathematics teaching and learning. A place where students do not feel anxious or scared to share and where learning from your peers is an everyday practice.
Hadn’t seen this hashtag until today! #RoughDraftMath so excited! I will be purchasing @MandyMathEd ‘s book ASAP. Was just talking with my PST this week about the importance of allowing Sts to draft and redraft like we do in English. https://t.co/hO4T2rjam7
— katherin cartwright (@kath_cartwright) October 17, 2019
“… teachers talk more explicitly about how people learn and the role of talk in learning, highlighting that learning takes time and that talking through in-progress ideas supports learning.”
Jansen, Cooper, Vascellaro and Wandless
In their paper, Jansen, Cooper, Vascellaro, and Wandless (2017) discuss the role of talk in learning and suggest three principles and practices to support rough-draft talk in mathematics:
-
Foster a culture supportive of intellectual risk taking.
This is where students are aware that initial discussions are “rough-drafts”. They are labelled as such and students are given time to share ideas with peers or in small groups (linking with talk move – turn and talk) and ideas are shared with no identification of ‘right’ or ‘wrong’. The teacher’s role during these discussions is to ask questions to guide students’s thinking and highlight important mathematical ideas. These “rough-draft” discussions can cycle through a number of times before final draft talk is undertaken.
-
Promote the belief that learning mathematics involves revising understanding over time.
This is a time to look over a common error or misunderstanding from an anonymous piece of work. Students revise a student’s explanation and share their ideas of how the error occurred proving reasoning that promotes mathematical precise language. Jansen et al. call this “My Favourite Rough-Draft” which is a modification of the “My Favourite No” routine. I’ve recommended the “My Favourite No” routine to teachers in the past, this video is a wonderful example of the routine and illustrates how the routine works as a formative assessment tool and effective feedback strategy.
-
Raise students’ statuses by expanding on what counts as a valuable contribution.
This principle provides space and a voice to those who may not usually participate in mathematical discourse around a problem. The teacher notices students’ wonderings or questions that arise around other students’ working out or strategies. Time is then taken to allow the students to voice their question as part of rough-draft talk and it is valued by the teacher. Using tasks that link to common misconceptions help in these discussions as many students may have the same questions. The rough-draft talk is seen as helpful and productive for the class and may help other students clarify their thinking.
“Engaging students in rough-draft talk promotes learning because whole-class discussion can foster understanding.”
Jansen, Cooper, Vascellaro and Wandless
It was great to put a name to the thinking I had been doing around the importance of revising in mathematics. Rough-draft talk gives permission for students to experience the productive struggle that we have been talking about in mathematics education recently. It removes the time limit to mathematical thinking. It squarely places the focus on continually developing a reasonable and measured solution, not parroting an immediate and finite numerical answer.
I also believe in rough-drafting in writing in mathematics. An essential aspect of sharing understanding, knowledge and reasoning in mathematics is through written responses. When students first start solving tasks their recording is often erratic and may be hard to follow or read later by the teacher if they weren’t with them when the student recorded their thinking. This doesn’t mean their solution is incorrect or that their working out and reasoning are somehow inferior to those who have ‘neat’ work, it just means they need time to re-draft.
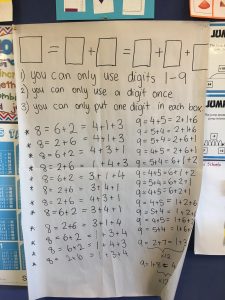
Class solutions for Make it Equal Open Middle task.
I used re-drafting recently with a Grade 3 and 4 class I taught using one of Robert Kaplinsky‘s openmiddle problems. During the lessons students found many solutions and used a range of problem solving strategies. A few students did see connections between their solutions and started using one solution to discover another, but not all students. This pattern-finding leads to generalisations and students can explore their conjectures and test them more easily once they order their solutions systematically. So I gave the class the challenge to re-record (re-draft and publish) their whole class solutions collectively over the next couple of days until I revisited the class. The image here is their re-drafted work. What an amazing piece of work to then be able to have further conversations about. The benefit of being able to extend a lesson to explore more complex mathematical ideas by using re-drafting is just the beginning!
I’m now looking forward to trying out more rough-draft talk and rough-draft writing in mathematics lessons both with children and with the pre-service teachers I work with at university. I love finding new ways of continually improving my teaching practice. If you’d like to find out more about rough-draft talk, follow Amanda on twitter (her handle is earlier in this blog) and her book on rough-draft talk is due out soon! I also found this blog about preventing student shut down in mathematics that also discusses Amanda Jansen’s work. You can also watch Amanda talking about rough-draft talk in this video.
References
Jansen, J., Cooper, B., Vascellaro, S., Wandless, P. (2017) Rough Draft Talk in the Mathematics Classroom. NCTM Teaching Mathematics in the Middle School Vol 22 Issue 5.