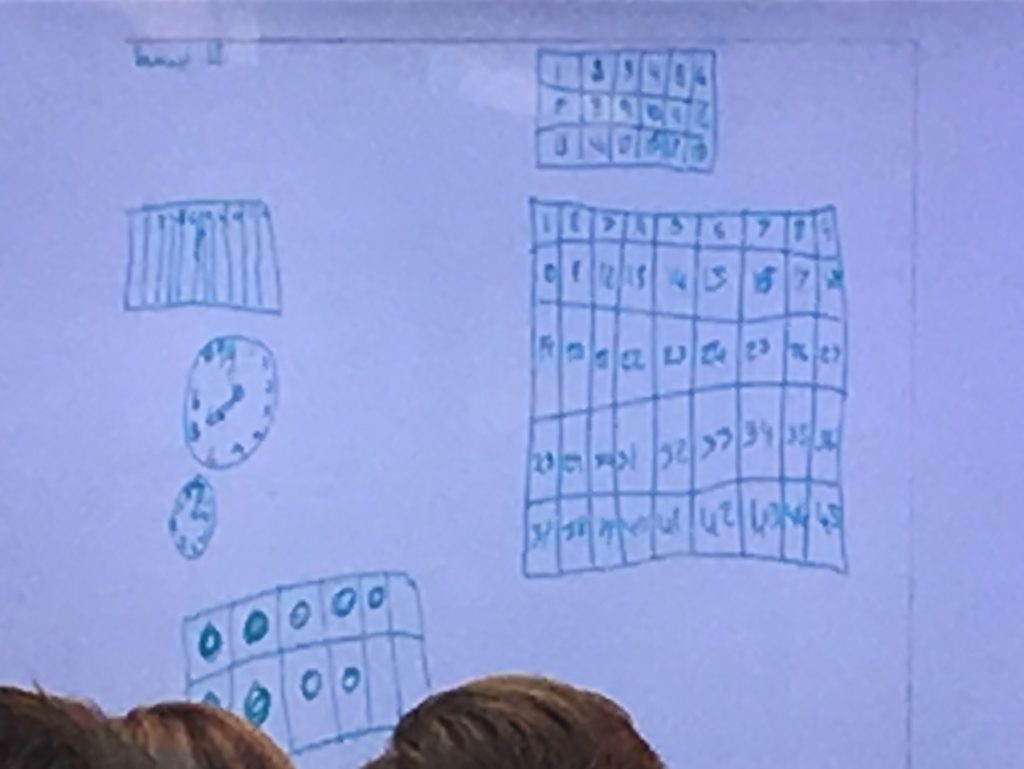As we start a new year with a new class, we often begin our teaching and learning cycle by asking ourselves “What do our students already know?” Building on prior knowledge, whether students have already been at school or not, is an essential practice as we guide students through the learning continuum of content. So what are some effective ways to assess students’ current mathematical knowledge? (that doesn’t require a ten page back-to-back test booklet!)
First things first. It is important to remind ourselves of the purpose of assessment. Assessment is the detective work of the teacher. It involves probing (asking the right questions), looking for clues (of misconceptions or understanding), and connecting the dots (where are the gaps between concepts or where to next). NESA (NSW Education Standards Authority) provide quality advice on assessment and remind us that we assess “to gather valid, reliable and useful information about student learning in order to:
- monitor student achievement in relation to outcomes
- guide future teaching and learning opportunities
- provide ongoing feedback to students to improve learning.”
NESA, (2019). Kindergarten to Year 6 assessment strategies (para. 1)
For this blog I’m focusing on the second dot point, to guide future teaching and learning opportunities. NESA list seven overarching strategies and provide assessment activity ideas for each assessment type. I have used a few of these strategies as categories to suggest specific mathematics tasks you might like to use in the first few weeks of school to start with assessment. These could be utilised and differentiated across all year grades (K to 6). Even if you feel they are not suited to your specific grade, all students sit along a shifting learning continuum, and therefore may display skills and understanding prior or beyond the grade they are in.
Teacher Observations
Listening to a student talk about their mathematics is just as important as listening to a student read in English. Mathematical fluency is often best observed and assessed orally as students describe their written and/or drawn work to communicate their understanding, reasoning and problem solving. You want to listen out for their use of language, both mathematics-specific and the certainty with which they speak “I know that…”
A good hands-on task to get students talking about what they are doing is the Third Dimension task from nrich.maths.org This task provide students with 4 interlocking (unifix) cubes and shows them one way to arrange the cubes. The question is then: How many other arrangements of 4 cubes can you find? The nrich version of this task includes students drawing a 2D diagram of the 3D arrangements on isometric dot paper – this could just be used for students in year 4 upwards. All students should be given enough cubes to make multiple representations. Photos can be taken, students can voice record via an iPad their thinking, or the teacher can have one-on-one discussions about their findings.
Peer and self-assessment
To have students judge their own work or the work of others, there needs to be a classroom culture that is supportive of differences in learning, a place where mistakes are part of the learning process. The comments need to be scaffolded around ‘strengths’ and ‘suggestions’ I often have students use the terms ‘notice and wonder’ to keep comments appropriate. Gallery Walks are a great way for students to peer assess.
I first read about gallery walks from this paper from the Ontario Ministry of Education. Students work on a task collaboratively, then walk around in pairs to provide comments on others’ work, then return to reflect on their own work afterwards.
One task I have used regularly in the past for gallery walks is from Peter Sullivan and Pat Lilburn’s book Open-Ended Maths Activities. I have included here an image of the question and a solution by year 5 students. Other students then used post it notes to add comments, looking at the solutions and strategies that may be similar or different to theirs.
Collaborative activities
The above-mentioned gallery walk task could also be seen as a collaborative task as students are working in pairs or small groups. Avenues for collaborative tasks in mathematics are extensive. Any time students are asked to think-pair-share or brainstorm together are assessment opportunities. STEM inquiry tasks also provide space for students to collaborate mathematically. STEM problem solving tasks such as; testing the strength of a sheet of paper, building the tallest spaghetti tower, creating the fastest balloon-powered plane, or building a paddle-pop stick bridge, all include mathematical concepts that could be assessed during the collaboration.
Here are a few more mathematics-focused collaborative tasks to use as assessments:
- Always, sometimes or never? There are many variations to this task and you can even create your own statements about any given concept
- Barrier Tasks – where students have a barrier up between them then create a picture or build a 3D construction then give instructions to each other to build their structure/ draw their design
- Cooperative tasks – you may have books with these ideas in your school teacher reference library like “Group Solutions” or “Cooperative Tasks”
Collection of student work
This is probably the most common way that data is collected from students in mathematics assessment. When I talk about student work though, it’s not just ‘pen and paper’. NESA’s Kindergarten to Year 6 assessment page offers suggestions of a wide variety of other student work samples that could be collected. I still make use of paper work samples during assessment, but generally, the paper starts out blank. It is important to allow students to speak for themselves in sharing their mathematical knowledge and understanding and this includes what they produce on the paper. I avoid pre-made work sheets or assessments, placing greater emphasis on open exploration tasks that do not corner students’ thinking into just answering the questions on the page.
Mathematics is about reasoning, pattern finding and making generalisations. Students need to be able to make connections between language, pictorial, symbolic and numerical representations. Students need to develop their knowledge of the structural quality of numerical, spatial, geometric and measurement concepts and how to visualise these to use in abstract situations. Much of what a student understands about structure, is visible through their drawing representations. Professor Joanne Mulligan has conducted longitudinal research into students’ understanding of pattern and number structure. Many of Joanne’s research assessment tasks are about students’ drawings of mathematical concepts. Here are a few that I would use at the beginning of the year to assess my students (K to Year 6). A number of these also come from Associate Professor Amy MacDonald’s (@A_Mac_D_) research.
- Draw a clock
- Draw a ten frame
- Draw a calendar
- Draw a hundreds chart
- Draw a ruler
- Draw a protractor
- Draw something tall and something short
- Draw something heavy and something light
If you are interested in either Amy’s or Joanne’s research, see the reference section below. I also wrote a blog that included Joanne Mulligan’s keynote at the Making 2020 count conference I attended in 2019. The use of students’ drawings is a great way to start with assessment in your classroom. It allows for student autonomy, creativity, and is less likely to cause mathematics anxiety that many traditional mathematics ‘tests’ do. It is also a great assessment that could be used for comparison at the end of the year with the same task to observe growth.
References
Erikson Institute – Early Math Collaborative videos of Joanne Mulligan talking about her research on early number patterns
MacDonald, A. (2013). Using children’s representations to investigate meaning-making in mathematics. Australasian Journal of Early Childhood, 38(2), 65-73.
Mulligan, J. (2010). Reconceptualising early mathematics learning.
Mulligan, J., Mitchelmore, M., Kemp, C., Marston, J., & Highfield, K. (2008). Encouraging Mathematical Thinking through Pattern & Structure: An Intervention in the First Year of Schooling. Australian Primary Mathematics Classroom, 13(3), 10-15.