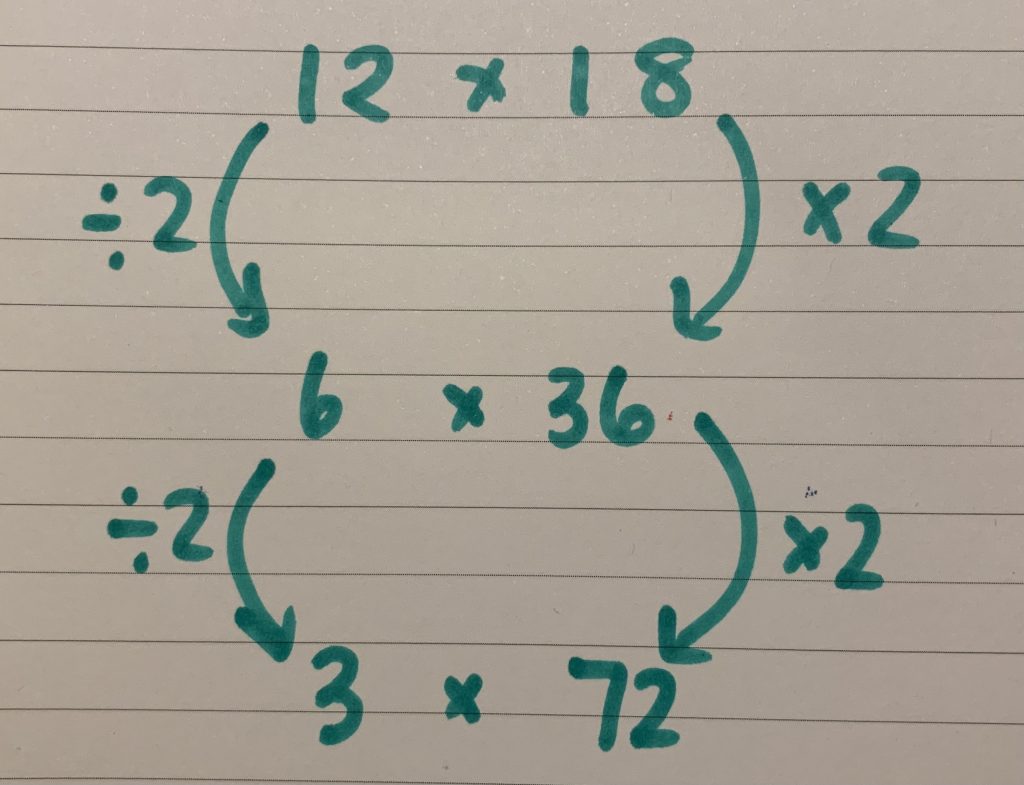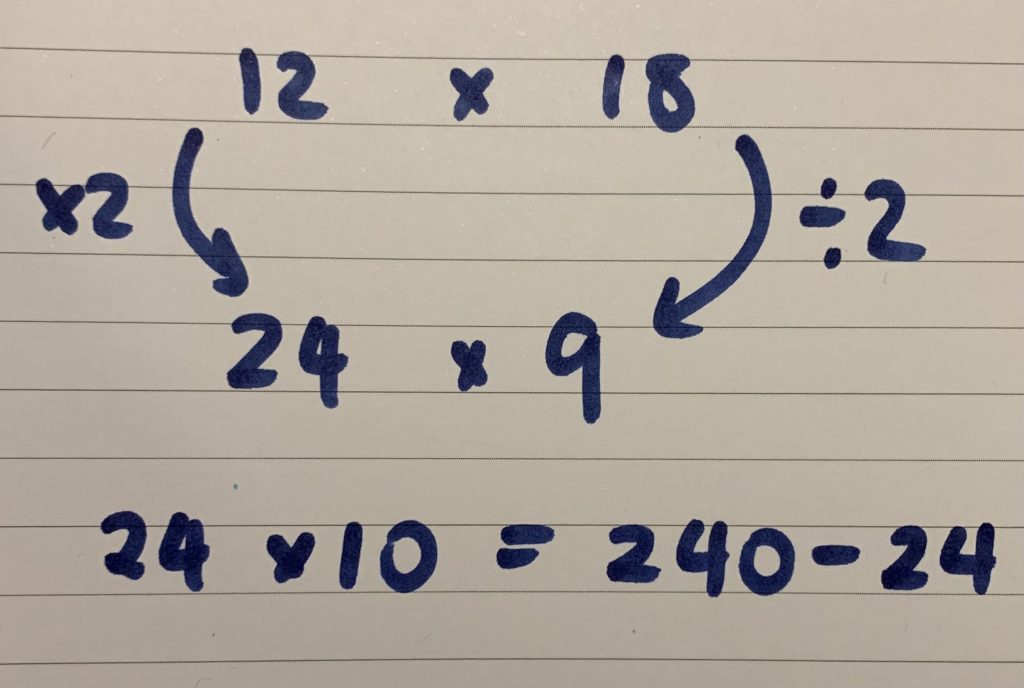If you’re teaching Year 5 or Year 6, then this question is one I’d ask your students this week. Last week when I was talking with a Year 5 student, we needed to solve 12 x 18 as part of a larger problem. When I asked, do you know how to work out 12 x 18, the response was: “I don’t know my 12 times tables”.
In November last year I wrote a blog titled If they just knew their times tables. When the student mention not knowing their times tables, it reminded me of all the reasons I prefer to teach through flexible strategies and conceptual understanding than by blind memorisation. For one, even if they knew their multiples of 12, this probably wouldn’t have assisted in solving 12 x 18 – unless they conceptually understood what to do next when they got to 12 x 12. Just knowing times tables doesn’t always help solve multiplication problems that build on this mathematical knowledge.
By the end of Year 6 (in ACARA’s Australian Curriculum), students should have a range of strategies to use to solve two-digit by two-digit multiplication problems:
Select and apply efficient mental and written strategies and appropriate digital technologies to solve problems involving all four operations with whole numbers, applying a range of strategies to solve realistic problems and commenting on the efficiency of different strategies (ACMNA123).
Interestingly, if we go back to Year 4 in the Australian Curriculum, some important strategies are mentioned that probably need to be getting more air-time in primary classrooms. This is not to say that inefficient strategies are being taught, just that when the vertical algorithm or learning multiplication facts as stand-alone facts is the focus – the flexibility required to solve 12 x 18 may not be all students’ comfort zone.
Develop efficient mental and written strategies and use appropriate digital technologies for multiplication and for division where there is no remainder, using known facts and strategies, such as commutativity, doubling and halving for multiplication, and connecting division to multiplication when there is no remainder (ACMNA076).
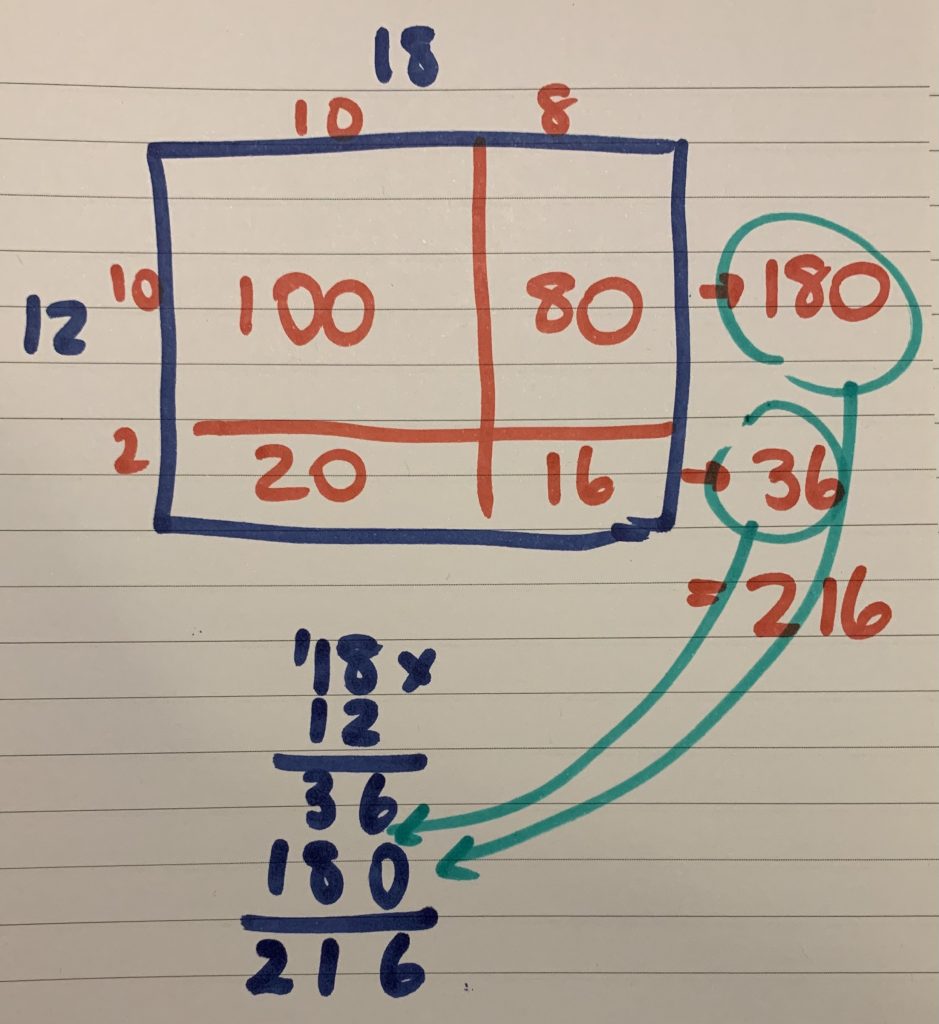
So what should we be expecting students in primary grades (Year 5 and Year 6 specifically) to know or be doing to solve 12 x 18? I think to begin with one of the most important things we can teach students is to stop and think – what do I already know about these numbers that can help me? The student I was talking to knew both numbers were even but didn’t know how that might help. The student suggested maybe timesing [sic] the 2 by the 1 and the 1 by the 8. Although this might not yield a correct solution, it shows the student understands that multiplication involves both numbers in the equation. The student was also able to give me an estimate about what might be a reasonable answer, the student suggested 204. This is quite a good estimate and shows an understanding of approximation of about 10 x 20. What strategies did we then talk about?
Using the area model – introducing students to the connection between area and multiplication helps with visualising ‘how big’ the numbers are and works with students knowledge of partitioning numbers by the place value parts.
This type of strategy then leads well into the algorithm as students can ‘see’ where the numbers come from.
Doubling and halving – this is a perfect strategy to apply especially when both numbers are even. This makes the problem easier and helps students get to more ‘friendly’ numbers to work with. They may still use some repeated addition to assist in the process but they are also building skills in dividing and multiplying by two.
Doubling and halving and compensation – If the student doubled the 12 instead, this brings to the fore another great strategy, compensation. Having 24 x 9 doesn’t lead itself to doubling and halving again (unless you like working with decimals!) but 9 is close to 10. Students can then do 24 x 10 and subtract one group of 24.
Focusing on students strategies and working with their misconceptions reminds me of a video Tierney Kennedy (@kennedy_tierney) shares where students are trying to solve 23 x 35 (second video on this page). I recommend watching this video and seeing if any of your own students have similar ideas and misconceptions about multiplication. Using questions like the one shared in this blog on a regular basis, to build efficient strategies, will develop students’ comfort zone with more advanced, flexible strategies. Jo Boaler’s (@joboaler) video about Stanford students solving 18 x 5 is also a good one to view. Pam Harris (@pwharris) shares her #MathStratChat weekly, these are great questions to use with students and so are the suggested ways to solve them! I particularly like her new thread of “what pings for you when you hear…” I think this is a great way to engage students in activating prior knowledge before they try to solve a task.
I asked what pings for you when you see/hear 90.
— Pam Harris (@pwharris) April 23, 2021
Here are some favs! So cool!
Did we miss any?#MTBoS #ITeachMath #MathIsFigureOutAble #Elemmathchat #MSmathchat #HSmathchat pic.twitter.com/VNFpfaVWbp
If the student did know 12 x 12 is 144 – then what? Do they know what’s left to work out? Do they know to work out 12 x 6 and add it on? This version of partial products would be just as efficient. These strategies also become super helpful when students need to apply their multiplicative thinking skills to solving problems involving volume (three-dimensions). So if you teach Year 5 or Year 6, I set you the challenge to give this question a go. Ask your students, “how would you solve 12 x 18?” I’m on Twitter (@kath_cartwright) so if you have any responses you’d like to share please do! Then we can keep the conversation going.
